Trigonometry/Solving Trigonometric Equations

Trigonometric equations are equations including trigonometric functions. If they have only such functions and constants, then the solution involves finding an unknown which is an argument to a trigonometric function.

Basic trigonometric equations

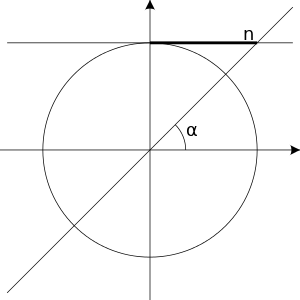
sin(x) = n

$n$	$\sin (x)=n$
$|n|<1$	$\begin{array}{c}x=\alpha +2k\pi \\ x=\pi -\alpha +2k\pi \\ \alpha \in [-\frac{\pi }{2},\frac{\pi }{2}]\end{array}$
$n=-1$	$x=-\begin{array}{c}\frac{\pi }{2}\end{array}+2k\pi$
$n=0$	$x=k\pi$
$n=1$	$x=\begin{array}{c}\frac{\pi }{2}\end{array}+2k\pi$
$|n|>1$	$x\in \varnothing$

The equation $\sin (x)=n$ has solutions only when $n$ is within the interval $[-1,1]$ . If $n$ is within this interval, then we first find an $\alpha$ such that:

$\alpha =\arcsin (n)$

The solutions are then:

$x=\alpha +2k\pi$

$x=\pi -\alpha +2k\pi$

Where $k$ is an integer.

In the cases when $n$ equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right.

For example, to solve:

$\sin \left(\frac{x}{2}\right)=\frac{\sqrt{3}}{2}$

First find $\alpha$ :

$\alpha =\arcsin \left(\frac{\sqrt{3}}{2}\right)=\frac{\pi }{3}$

Then substitute in the formulae above:

$\frac{x}{2}=\frac{\pi }{3}+2k\pi$

$\frac{x}{2}=\pi -\frac{\pi }{3}+2k\pi$

Solving these linear equations for $x$ gives the final answer:

$x=\frac{2\pi }{3}(1+6k)$

$x=\frac{4\pi }{3}(1+3k)$

Where $k$ is an integer.

cos(x) = n

$n$	$\cos (x)=n$
$|n|<1$	$\begin{array}{c}x=\pm \alpha +2k\pi \\ \alpha \in [0,\pi ]\end{array}$
$n=-1$	$x=\pi +2k\pi$
$n=0$	$x=\begin{array}{c}\frac{\pi }{2}\end{array}+k\pi$
$n=1$	$x=2k\pi$
$|n|>1$	$x\in \varnothing$

Like the sine equation, an equation of the form $\cos (x)=n$ only has solutions when n is in the interval $[-1,1]$ . To solve such an equation we first find one angle $\alpha$ such that:

$\alpha =\arccos (n)$

Then the solutions for $x$ are:

$x=\pm \alpha +2k\pi$

Where $k$ is an integer.

Simpler cases with $n$ equal to 1, 0 or -1 are summarized in the table on the right.

tan(x) = n

$n$	$\tan (x)=n$
General case	$\begin{array}{c}x=\alpha +k\pi \\ \alpha \in [-\frac{\pi }{2},\frac{\pi }{2}]\end{array}$
$n=-1$	$x=-\begin{array}{c}\frac{\pi }{4}\end{array}+k\pi$
$n=0$	$x=k\pi$
$n=1$	$x=\begin{array}{c}\frac{\pi }{4}\end{array}+k\pi$

An equation of the form $\tan (x)=n$ has solutions for any real $n$ . To find them we must first find an angle $\alpha$ such that:

$\alpha =\arctan (n)$

After finding $\alpha$ , the solutions for $x$ are:

$x=\alpha +k\pi$

When $n$ equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.

cot(x) = n

$n$	$\cot (x)=n$
General case	$\begin{array}{c}x=\alpha +k\pi \\ \alpha \in [0;\pi ]\end{array}$
$n=-1$	$x=-\begin{array}{c}\frac{3\pi }{4}\end{array}+k\pi$
$n=0$	$x=\begin{array}{c}\frac{\pi }{2}\end{array}+k\pi$
$n=1$	$x=\begin{array}{c}\frac{\pi }{4}\end{array}+k\pi$

The equation $\cot (x)=n$ has solutions for any real $n$ . To find them we must first find an angle $\alpha$ such that:

$\alpha =\mathrm{arccot}(n)$

After finding $\alpha$ , the solutions for $x$ are:

$x=\alpha +k\pi$

When $n$ equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.

csc(x) = n and sec(x) = n

The trigonometric equations $\csc (x)=n$ and $\sec (x)=n$ can be solved by transforming them to other basic equations:

$\csc (x)=n\iff \frac{1}{\sin (x)}=n\iff \sin (x)=\frac{1}{n}$

$\sec (x)=n\iff \frac{1}{\cos (x)}=n\iff \cos (x)=\frac{1}{n}$

Further examples

Generally, to solve trigonometric equations we must first transform them to a basic trigonometric equation using the [[../Trigonometric_Identities_Reference|trigonometric identities]]. This sections lists some common examples.

a sin(x)+b cos(x) = c

To solve this equation we will use the identity:

$a\sin (x)+b\cos (x)=\sqrt{a^2+b^2}\sin (x+\alpha )$

$\alpha =\{\begin{array}{cc}\arctan \left(\frac{b}{a}\right),& \text{if }a>0\\ \pi +\arctan \left(\frac{b}{a}\right),& \text{if }a<0\end{array}$

The equation becomes:

$\sqrt{a^2+b^2}\sin (x+\alpha )=c$

$\sin (x+\alpha )=\frac{c}{\sqrt{a^2+b^2}}$

This equation is of the form $\sin (x)=n$ and can be solved with the formulae given above.

For example we will solve:

$\sin (3x)-\sqrt{3}\cos (3x)=-\sqrt{3}$

In this case we have:

$a=1,b=-\sqrt{3}$

$\sqrt{a^2+b^2}=\sqrt{1^2+(-\sqrt{3}{)}^2}=2$

$\alpha =\arctan (-\sqrt{3})=-\frac{\pi }{3}$

Apply the identity:

$2\sin (3x-\frac{\pi }{3})=-\sqrt{3}$

$\sin (3x-\frac{\pi }{3})=-\frac{\sqrt{3}}{2}$

So using the formulae for $\sin (x)=n$ the solutions to the equation are:

$3x-\frac{\pi }{3}=-\frac{\pi }{3}+2k\pi \iff x=\frac{2k\pi }{3}$

$3x-\frac{\pi }{3}=\pi +\frac{\pi }{3}+2k\pi \iff x=\frac{\pi }{9}(6k+5)$

Where $k$ is an integer.