Waves/Derivatives
Math Tutorial -- Derivatives
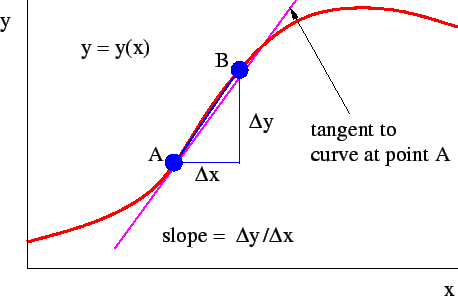
Figure 1.15: Estimation of the derivative, which is the slope of the tangent line. When point B approaches point A, the slope of the line AB approaches the slope of the tangent to the curve at point A.
This section provides a quick introduction to the idea of the derivative. For a more detailed discussion and exploration of the differentiation and of Calculus, see Calculus and Differentiation.
Often we are interested in the slope of a line tangent to a function at some value of . This slope is called the derivative and is denoted . Since a tangent line to the function can be defined at any point , the derivative itself is a function of :
- (2.25)
As figure 1.15 illustrates, the slope of the tangent line at some point on the function may be approximated by the slope of a line connecting two points, A and B, set a finite distance apart on the curve:
- (2.26)
As B is moved closer to A, the approximation becomes better. In the limit when B moves infinitely close to A, it is exact.
Table of Derivatives
Derivatives of some common functions are now given. In each case is a constant.
| Table of Derivatives | |
|---|---|
| where both xc and cxc−1 are defined. | |
| x > 0 | |
| c > 0 | |
| c > 0, c ≠ 1 | |
The product and chain rules are used to compute the derivatives of complex functions. For instance,
and