Control Systems/Examples/Second Order Systems

Second Order Systems: Examples

Example 1

A damped control system for aiming a hydrophonic array on a minesweeper vessel has the following open-loop transfer function from the driveshaft to the array.

$G(s)=\frac{K}{J{s}^2+K_{d}s}$

The gain parameter K can be varied. The moment of inertia, J, of the array and the force due to viscous drag of the water, K_d are known constants and given as:

• $J=9Nm{s}^{2}ra{d}^{-1}$
• $K_d=2Nmsra{d}^{-1}$

Tasks

1. The system is arranged as a closed loop system with unity feedback. Find the value of K such that, when the input is a unit step, the closed loop response has at most a 50% overshoot (approximately). You may use standard response curves. Should K be greater or less than this value for less overshoot?
2. Find the corresponding time-domain response of the system.
3. The system is now given an input of constant angular velocity, V. For the limiting value of K found above, calculate the maximum value of V such that the array follows the input with at most 5° error.

Task 1

First, let us draw the block diagram of the system. We know the open-loop transfer function, and that there is unit feedback. Therefore, we have:

The closed-loop gain is given by:

$H(s)$	$=\frac{G(s)}{1+G(s)}$
	$=\frac{\frac{K}{J{s}^2+K_{d}s}}{\frac{J{s}^2+K_{d}s+K}{J{s}^2+K_{d}s}}$
	$=\frac{K}{J{s}^2+K_{d}s+K}$

We now need to express the closed-loop transfer function in the standard second order form.

$\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$	$=\frac{K}{J{s}^2+K_{d}s+K}$
	$=\frac{\frac{K}{J}}{s^2+\frac{K_d}{J}s+\frac{K}{J}}$

We can now express the natural frequency ω_n and damping ratio, ζ:

${\omega }_n^2=\frac{K}{J}=\frac{K}{9}$

$2\zeta {\omega }_n=\frac{K_d}{J}$

$\zeta =\frac{K_d}{2J}\sqrt{\frac{J}{K}}=\frac{K_d}{2}\sqrt{\frac{1}{KJ}}=\frac{1}{3\sqrt{K}}$

We now look at the standard response curves for second order systems.

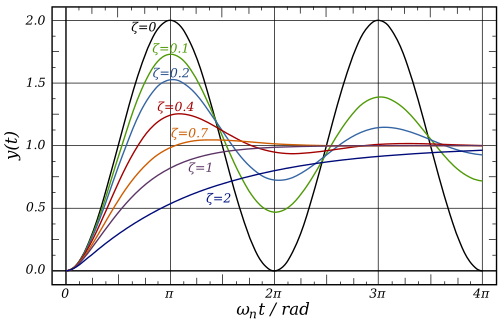
We see that for 50% overshoot, we need ζ=0.2 or more.

$\zeta =\frac{1}{3\sqrt{K}}\ge \frac{1}{5}$

$K\le \frac{25}{9}$

This is the maximum permissible value, thus K should be less than this value for less overshoot. We can now evaluate the natural frequency fully:

${\omega }_n=\frac{5}{9}$

Task 2

The output of the second order system is given by the following equation:

$y(t)$	$=1-\frac{1}{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{n}t}\sin (\sqrt{1-{\zeta }^2}{\omega }_{n}t+{\sin }^{-1}\sqrt{1-{\zeta }^2})$
	$=1-\frac{1}{\sqrt{0.96}}{e}^{-t/9}\sin (\frac{5\sqrt{0.96}}{9}t+{\sin }^{-1}\sqrt{0.96})$
	$=1-1.02e^{-t/9}\sin (0.544t+0.436\pi )$

We can plot the output of this system:

Task 3

The tracking error signal, E(s), is equal to the output's deviation from the input.

$E(s)=R(s)-Y(s)$

Now, we can find the gain from the reference input, R(s) to the error tracking signal:

$\frac{E(s)}{R(s)}=\frac{R(s)-Y(s)}{R(s)}$

The gain from the input to the error tracking signal of a unity feedback system like this is simply $\frac{1}{1+G(s)}$.

$\frac{E(s)}{R(s)}$	$=\frac{1}{1+\frac{K}{9s^2+2s}}$
	$=\frac{9s^2+2s}{9s^2+2s+2.78}$

Now, R(s) is given by the Laplace transform of a ramp of slope V:

$R(s)=\frac{v}{s^2}$

We now use the final value theorem to find the value of E(s) in the steady state:

$\underset{t\to \mathrm{\infty }}{\lim }e(t)$	$=\underset{s\to 0}{\lim }sE(s)$
	$=\underset{s\to 0}{\lim }s\frac{9s^2+2s}{9s^2+2s+2.78}\frac{V}{s^2}$
	$=\frac{2V}{2.78}$

We require this to be less than $5^{\circ }=\frac{5\pi }{180}\text{rad}$

$V\le \frac{2.78}{2}\times \frac{5\pi }{180}=0.12\text{rad/s}$