Digital Circuits/CORDIC

A CORDIC (standing for COordinate Rotation DIgital Computer) circuit serves to compute several common mathematical functions, such as trigonometric, hyperbolic, logarithmic and exponential functions.

Application

A CORDIC uses only adders and bitshifts to compute the results, with the benefit that it can therefore be implemented using relatively basic hardware.

Methods such as power series or table lookups usually need multiplications to be performed. If a hardware multiplier is not available, a CORDIC is generally faster, but if a multiplier can be used, other methods may be faster.

CORDICs can also be implemented in many ways, including a single-stage iterative method, which requires very few gates when compared to multiplier circuits. Also, CORDICs can compute many functions with precisely the same hardware, so they are ideal for applications with an emphasis on reduction of cost (e.g. by reducing gate counts in FPGAs) over speed. An example of this priority is in pocket calculators, where CORDICs are very frequently used.

History

The CORDIC was first invented in 1959 by J.E. Volder, in the aeroelectronics departments of Convair, and was designed for the B-58 Hustler bomber's navigational computer to replace an analogue resolver, a device that computed trigonometric functions (Circular CORDIC).

In 1971, J.S. Walther, at Hewlett-Packard, extended the method to calculate hyperbolic functions, natural logarithms, natural exponentials, multiplications, divisions, and square roots (Linear CORDIC and Hyperbolic CORDIC).

In 2019, based on Hyperbolic CORDIC, Yuanyong Luo et al. further proposed a Generalized Hyperbolic CORDIC (GH CORDIC) to directly compute logarithms and exponentials with an arbitrary fixed base. Theoretically, Hyperbolic CORDIC is a special case of GH CORDIC.

General Concept

Consider the following rotations of vectors:


Start at (1, 0) Rotate by θ We get (cosθ, sinθ)	Start at (1, y) Rotate until y = 0 The rotation is tan⁻¹y

If we were to have a computationally efficient method of rotating a vector, we can directly evaluate sine, cosine and arctan functions. However, rotation by an arbitrary angle is non-trivial (you have to know the sine and cosines, which is precisely what we don't have). We use two methods to make it easier:

Instead of performing rotations, we perform "pseudorotations", which are easier to compute.
Construct the desired angle θ from a sum of special angles, α_i:

θ = α_{1} + α_{2} + \dots + α_{m}

The diagram belows shows a rotation and pseudo-rotation of a vector of length R_i about an angle of a_i about the origin:

A rotation about the origin produces the following co-ordinates:

x_{i + 1} = x_{i} \cos α_{i} - y_{i} \sin α_{i}

y_{i + 1} = y_{i} \cos α_{i} + x_{i} \sin α_{i}

θ_{i + 1} = θ_{i} + α_{i}

Recall the identity $\cos θ \equiv 1 / \sqrt{1 + \tan^{2} θ}$ .

x_{i + 1} = (x_{i} - y_{i} \tan α_{i}) / \sqrt{1 + \tan^{2} α_{i}}

y_{i + 1} = (y_{i} + x_{i} \tan α_{i}) / \sqrt{1 + \tan^{2} α_{i}}

Our strategy will be to eliminate the factor of $1 / \sqrt{1 + \tan^{2} α_{i}}$ and somehow remove the multiplication by $\tan α_{i}$ . A pseudo-rotation produces a vector with the same angle as the rotated vector, but with a different length. In fact, the pseudo-rotation changes the length to:

R_{i + 1} = \frac{R_{i}}{\cos α_{i}} = R_{i} \sqrt{1 + \tan^{2} α_{i}}

Thus we now have these co-ordinates following a pseudo-rotation:

x_{i + 1}^{'} = (x_{i} - y_{i} \tan α_{i})

y_{i + 1}^{'} = (y_{i} + x_{i} \tan α_{i})

θ_{i + 1} = θ_{i} - α_{i}

The pseudo-rotation has succeeded in removing our length-factor, which would have required a costly division operation. However, the vector will grow by a factor of K over a sequence of n pseudo-rotations:

K = \prod_{i = 0}^{n - 1} \sqrt{1 + \tan^{2} α_{i}}

The co-ordinates following the n pseudo-rotations are then:

x_{n} = K (x_{i} \cos \sum_{i = 0}^{n - 1} α_{i} - y_{i} \sin \sum_{i = 0}^{n - 1} α_{i})

y_{n} = K (y_{i} \cos \sum_{i = 0}^{n - 1} α_{i} + x_{i} \sin \sum_{i = 0}^{n - 1} α_{i})

θ_{n} = θ_{i} - \sum_{i = 0}^{n - 1} α_{i}

If the angles are always the same set, then K is fixed, and can be accounted for later. We choose these angle according to two criteria:

We must also choose the angles so that any angle can be constructed from the sum of all them, with appropriate signs.
We make all $\tan α_{i}$ a power of 2, so that the multiplication can be performed by a simple logical shift of a binary number.

The tangent function has a monotonically increasing gradient on the interval [0, π/2], so the tangent of a given angle is always less than twice the tangent of half the angle. This means that if we make the angles $α_{i} = \tan^{- 1} 2^{- i}$ , we can satisfy both criteria. Note that the tangent function is odd, which means that to pseudo-rotate the other way, you just subtract, rather than add, the tangent of the angle.

i	α_i = tan⁻¹ (2⁻ⁱ)
i	Degrees	Radians
0	45.00	0.7854
1	26.57	0.4636
2	14.04	0.2450
3	7.13	0.1244
4	3.58	0.0624
5	1.79	0.0312
6	0.90	0.0160
7	0.45	0.0080
8	0.22	0.0040
9	0.11	0.0020

In step i of the process, we pseudo-rotate by $d_{i} 2^{- i}$ , where $d_{i}$ is the direction (or sign) of the rotation, which will be chosen at each step to force the angle to converge to the desired final rotation. For example, consider a rotation of 28°:

28 \approx 45.0 - 26.57 + 14.04 - 7.13 + 3.58 - 1.79 + 0.90 - 0.45 + 0.22 + 0.11

28 \approx 27.91

The more steps we take, the better the approximation that we can make by successive rotations. Thus, we have the following iterative co-ordinate calculation:

x_{i + 1} = x_{i} - d_{i} y_{i} 2^{- i}

y_{i + 1} = y_{i} + d_{i} x_{i} 2^{- i}

θ_{i + 1} = θ_{i} - d_{i} α_{i}

In order to achieve k bit of precision, k iterations are needed, because $\tan^{- 1} 2^{- i} ⪅ 2^{- i}$ , converging as i increases.

Using CORDICs

CORDICs can be used to compute many functions. A CORDIC has three inputs, x₀, y₀, and z₀. Depending on the inputs to the CORDIC, various results can be produced at the outputs x_n, y_n, and z_n. Template:Clear

Using CORDIC in rotation mode

$x_{i + 1} = x_{i} - d_{i} y_{i} 2^{- i}$
$y_{i + 1} = y_{i} + d_{i} x_{i} 2^{- i}$
$z_{i + 1} = z_{i} - d_{i} α_{i}$

$x_{n} = K (x_{0} \cos z_{0} - y_{0} \sin z_{0})$
$y_{n} = K (y_{0} \cos z_{0} + x_{0} \sin z_{0})$
$z_{n} = 0$

For convergence of z_n to 0, choose $d_{i} = sgn z_{i}$ .

If we start with x₀ = 1/K and y₀=0, at the end of the process, we find x_n=cos z₀ and y_n=sin z₀.

The domain of convergence is $- 99 . 7^{\circ} < z_{0} < 99 . 7^{\circ}$ because 99.7° is the sum of all angles in the list.

Using CORDIC in vectoring mode

$x_{i + 1} = x_{i} - d_{i} y_{i} 2^{- i}$
$y_{i + 1} = y_{i} + d_{i} x_{i} 2^{- i}$
$z_{i + 1} = z_{i} - d_{i} α_{i}$

$x_{n} = K \sqrt{x^{2} + y^{2}}$
$y_{n} = 0$
$z_{n} = z_{0} + \tan^{- 1} (y_{0} / x_{0})$

For convergence of y_n to 0, choose $d_{i} = - sgn (y_{i})$ .

If we start with x₀ = 1 and z₀ = 0, we find z_n=tan⁻¹y₀

Implementations of CORDICs

Bit-parallel, unrolled

Bit-parallel, iterative

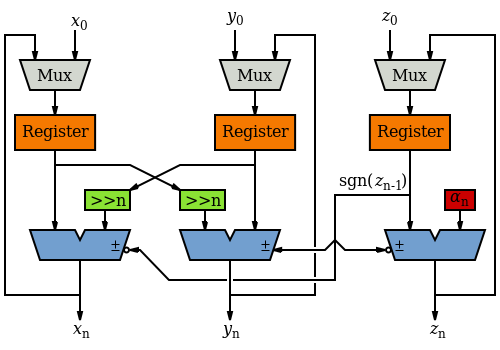
If a high speed is not required, this can be implemented with a single adder and a single shifter.

Bit-serial

The Universal CORDIC

By introducing a factor μ, we can also cater for linear and hyperbolic functions:

x_{i + 1} = x_{i} - μ d_{i} y_{i} 2^{- i}

y_{i + 1} = y_{i} + d_{i} x_{i} 2^{- i}

z_{i + 1} = z_{i} - d_{i} α_{i}

Summary of Universal CORDIC implementations

x_{i + 1} = x_{i} - μ d_{i} y_{i} 2^{- i}

y_{i + 1} = y_{i} + d_{i} x_{i} 2^{- i}

z_{i + 1} = z_{i} - d_{i} α_{i}

Mode	Rotation	Vectoring
Mode	$d_{i} = sgn (z_{i}), z \to 0$	$d_{i} = - sgn (y_{i}), y \to 0$
Circular μ = 1 α_i = tan⁻¹2⁻ⁱ
Linear μ = 0 α_i = 2⁻ⁱ
Hyperbolic μ = -1 α_i = tanh⁻¹2⁻ⁱ
In hyperbolic mode, iterations 4, 13, 40, 121, ..., j, 3j+1,... must be repeated. The constant K' given below accounts for this. K = 1.646760258121... 1/K = 0.607252935009... K' = 0.8281593609602... 1/K' = 1.207497067763...

Directly computable functions

$\sin z$	$\cos z$
$\tan^{- 1} z$	$\sinh z$
$\cosh z$	$\tanh^{- 1} z$
$y / x$	$x z$
$\tan^{- 1} (y / x)$	$\sqrt{x^{2} + y^{2}}$
$\sqrt{x^{2} - y^{2}}$	$e^{z} = \sinh z + \cosh z$

Indirectly computable functions

In addition to the above functions, a number of other functions can be produced by combining the results of previous computations:

$\tan z = \frac{\sin z}{\cos z}$	$\cos^{- 1} w = \tan^{- 1} \frac{\sqrt{1 - w^{2}}}{w}$
$\tanh z = \frac{\sinh z}{\cosh z}$	$\sin^{- 1} w = \tan^{- 1} \frac{w}{\sqrt{1 - w^{2}}}$
$\ln w = 2 \tanh^{- 1} \frac{w - 1}{w + 1}$	$\log_{b} w = \frac{\ln w}{\ln b}$
$w^{t} = e^{t \ln w}$	$\cosh^{- 1} = \ln (w + \sqrt{w^{2} - 1})$
$\tan^{- 1} (y / x)$	$\sinh^{- 1} = \ln (w + \sqrt{w^{2} + 1})$
$\sqrt{x^{2} - y^{2}}$	$\sqrt{w} = \sqrt{(w + 1 / 4)^{2} - (w - 1 / 4)^{2}}$

Digital Circuits/CORDIC

Contents

Application

History

General Concept