Abstract Algebra/Group Theory/Normal subgroups and Quotient groups

Template:TOC right In the preliminary chapter we discussed equivalence classes on sets. If the reader has not yet mastered this notion, he/she is advised to do so before starting this section.

Normal Subgroups

Recall the definition of kernel in the previous section. We will exhibit an interesting feature it possesses. Namely, let $ak,k\in \ker \varphi \le G$ be in the coset $a\ker \varphi$. Then there exists a $k^{\prime }\in \ker \varphi$ such that $k^{\prime }a=ak$ for all $a\in G$. This is easy to see because a coset of the kernel includes all elements in $G$ that are mapped to a particular element. The kernel inspires us to look for what are called normal subgroups.

Definition 1: A subgroup $N\le G$ is called normal if $gN{g}^{-1}=N$ for all $g\in G$. We may sometimes write $N⊴G$ to emphasize that $N$ is normal in $G$.

Theorem 2: A subgroup $N\le G$ is normal if and only if $gN=Ng$ for all $g\in G$.

Proof: By the definition, a subgroup is normal if and only if $gN{g}^{-1}=N$ since conjugation is a bijection. The theorem follows by multiplying on the right by $g$. Template:Unicode

We stated that the kernel is a normal subgroup in the introduction, so we had better well prove it!

Theorem 3: Let $\varphi :G\to G^{\prime }$ be any homomorphism. Then $\ker \varphi \le G$ is normal.

Proof: Let $k\in \ker \varphi$ and $g\in G$. Then $\varphi (gk{g}^{-1})=\varphi (g)e^{\prime }\varphi (g{)}^{-1}=e^{\prime }$, so $gk{g}^{-1}\in \ker \varphi$, proving the theorem. Template:Unicode

Theorem 4: Let $G,G^{\prime }$ be groups and $\varphi :G\to G^{\prime }$ a group homomorphism. Then if $H$ is a normal subgroup of $\mathrm{i}\mathrm{m}\varphi$, then ${\varphi }^{-1}(H)$ is normal in $G$.

Proof: Let $g\in G$ and $h\in {\varphi }^{-1}(H)$. Then $\varphi (gh{g}^{-1})=\varphi (g)\varphi (h)\varphi (g{)}^{-1}\in H$ since $H$ is normal in $\mathrm{i}\mathrm{m}\varphi$, and so $gh{g}^{-1}\in {\varphi }^{-1}(H)$, proving the theorem. Template:Unicode

Theorem 5: Let $G,G^{\prime }$ be groups and $\varphi :G\to G^{\prime }$ a group homomorphism. Then if $H$ is a normal subgroup of $G$, $\varphi (H)$ is normal in $\mathrm{i}\mathrm{m}\varphi$.

Proof: Let $g^{\prime }\in \mathrm{i}\mathrm{m}\varphi$ And $h\in H$. Then if $g\in G$ such that $\varphi (g)=g^{\prime }$, we have $g^{\prime }\varphi (h){g^{\prime }}^{-1}=\varphi (g)\varphi (h)\varphi (g{)}^{-1}=\varphi (gh{g}^{-1})=\varphi (h^{\prime })\in \varphi (H)$ for some $h^{\prime }\in H$ since $H$ is normal. Thus $g^{\prime }\varphi (H){g^{\prime }}^{-1}=\varphi (H)$ for all $g^{\prime }\in \mathrm{i}\mathrm{m}\varphi$ and so $H$ is normal in $\mathrm{i}\mathrm{m}\varphi$. Template:Unicode

Corollary 6: Let $G,G^{\prime }$ be groups and $\varphi :G\to G^{\prime }$ a surjective group homomorphism. Then if $H$ is a normal subgroup of $G$, $\varphi (H)$ is normal in $G^{\prime }$.

Proof: Replace $\mathrm{i}\mathrm{m}\varphi$ with $G^{\prime }$ in the proof of Theorem 5. Template:Unicode

Remark 7: If $H$ is a normal subgroup of $G$ and $K$ is a normal subgroup of $H$, it does not necessarily imply that $K$ is a normal subgroup of $G$. The reader is invited to display a counterexample of this.

Theorem 8: Let $G$ be a group and $H,K$ be subgroups. Then

i) If $H$ is normal, then $HK=KH$ is a subgroup of $G$.

ii) If both $H$ and $K$ are normal, then $HK=KH$ is a normal subgroup of $G$.

iii) If $H$ and $K$ are normal, then $H\cap K$ is a normal subgroup of $G$.

Proof: i) Let $H$ be normal. First, since for each $k\in K$, there exists $h,h^{\prime }\in H$ such that $kh=h^{\prime }k$, so $KH=HK$. To show $HK$ is a subgroup, let $hk,h^{\prime }{k}^{\prime }\in HK$. Then $h^{\prime }{k}^{\prime }(hk{)}^{-1}=h^{\prime }{k}^{\prime }{k}^{-1}{h}^{-1}=h^{\prime }{h}^{\prime \prime }{k}^{\prime }{k}^{-1}\in HK$ for some $h^{\prime \prime }\in H$ since $H$ is normal, and so $HK$ is a subgroup.

ii) Let $g\in G$ and $hk\in HK$. Then since both $H$ and $K$ are normal, there exists $h^{\prime }\in H,k^{\prime }\in K$ such that $ghk{g}^{-1}=gh{g}^{-1}{k}^{\prime }=g{g}^{-1}{h}^{\prime }{k}^{\prime }=h^{\prime }{k}^{\prime }\in HK$. It follows that $gHK{g}^{-1}=HK$ and so $HK$ is normal.

iii) Let $g\in G$ and $h\in H\cap K$. Then $gh{g}^{-1}\in H$ since H is normal, and similarly $gh{g}^{-1}\in K$. Thus $gh{g}^{-1}\in H\cap K$ and it follows that $H\cap K$ is normal. Template:Unicode

Examples of Normal Subgroups

In the following, let $G$ be any group. Then $G$ has associated with it the following normal subgroups.

i) The center of $G$, denoted $Z(G)$, is the subgroup of elements which commute with all others. $Z(G)=\{z\in G\mid (\mathrm{\forall }g\in G)zg=gz\}$. That $Z(G)$ is a normal subgroup is easy to verify and is left to the reader.

ii) The commutator subgroup of $G$, denoted $G^{(1)}$ or $[G,G]$, is the subgroup generated by the subset $\{[g,h]\mid g,h\in G\}$ where $[g,h]=g^{-1}{h}^{-1}gh$ for all $g,h\in G$. For $s\in G$, we introduce the shorthand $sg{s}^{-1}=g^s$. Then we have $s[g,h]s^{-1}=[g^s,h^s]$, such that for any product of commutators $[g_1,h_1][g_2,h_2]...[g_n,h_n]$ where all elements are in $G$, we have $s[g_1,h_1][g_2,h_2]...[g_n,h_n]s^{-1}=[g_1^s,h_1^s][g_2^s,h_2^s]...[g_n^s,h_n^s]$, and so $G^{(1)}$ is normal.

Remark 9: We can iterate the commutator subgroup construction and define $G^{(0)}=G$ and $G^{(n)}=[G^{(n-1)},G^{(n-1)}]$ for all $n\in \mathbb{N}$. We will not use the commutator subgroup in future results in this book, so for us it is merely a curiosity.

Equivalence Relations on Groups

Why are normal subgroups important? In the preliminary chapter we discussed equivalence relations and the associated set of equivalence classes. If $G$ is a group and $\sim$ is an equivalence relation, when does $G/\sim$ admit a group structure? Of course we have to specify the multiplication on $G/\sim$. We will do so now.

Definition 10: Let $G$ be a group and $\sim$ is an equivalence relation on $G$, we define multiplication on the equivalence classes in $G/\sim$ such that for all $a,b\in G$,

$[a][b]=[ab]$

This is indeed the only natural way to do it. Take the two equivalence classes, choose representatives, compute their product and take its equivalence class. The alert reader will have only one thing on his/her mind: is this well defined? For a general equivalence relation, the answer is no. The reader is invited to come up with an example. What is more interesting is when is it well defined? By the definition above, we obviously need the projection map $\pi :G\to G/\sim$ defined by $a\mapsto [a]$ to be a homomorphism. We can in fact condense the requirements down to two, both having to do with cancellation laws.

Theorem 11: Let $G$ be a group and $\sim$ an equivalence relation on $G$. Then $G/\sim$ is a group under the natural multiplication if and only if for all $a,b,g\in G$

$a\sim b\iff ag\sim bg\wedge ga\sim gb$.

Proof: Assume $G/\sim$ is a group. Since $a\sim b\iff [a]=[b]$, the property follows from the cancellation laws in $G$. Assume now that the property holds. Then its multiplication rule is well defined, and must verify that $G/\sim$ is a group. Let $a,b,c\in G$, then associativity is inherited from $G$:

$([a][b])[c]=[ab][c]=[(ab)c]=[a(bc)]=[a][bc]=[a]([b][c])$.

The identity in $G/\sim$ is the equivalence class of $e\in G$, $[e]$:

$[e][a]=[ea]=[a]=[ae]=[a][e]$.

Finally, the inverse of $[a]$ is $[a^{-1}]$:

$[g][g^{-1}]=[g{g}^{-1}]=[e]=[g^{-1}g]=[g^{-1}][g]$.

So $G/\sim$ really defines a group structure, proving the theorem. Template:Unicode

We will call an equivalence relation $\sim$ compatible with $G$ if $G/\sim$ is a group. Then, $G/\sim$ is called the quotient group of $G$ by $\sim$. Also, as an immediate consequence, this makes $\pi :G\to G/\sim$ into a homomorphism, but not just any homomorphism! It satisfies a universal property!

Commutative diagram showing the universal property satisfied by the projection homomorphism.

Theorem 12: Let $\sim$ be en equivalence relation compatible with $G$, and $\varphi :G\to H$ a group homomorphism such that $a\sim b\Rightarrow \varphi (a)=\varphi (b)$. Then there exists a unique homomorphism $\tilde{\varphi }:G/\sim \to H$ such that $\varphi =\tilde{\varphi }\circ \pi$.

Proof: In the preliminary chapter on set theory, we showed the corresponding statement for sets, so we know that $\tilde{\varphi }$ exists as a function between sets. We have to show that it is a homomorphism. This follows immediately: since $\tilde{\varphi }([a])=\varphi (a)$ by commutativity, we have $\tilde{\varphi }([a])\tilde{\varphi }([b])=\varphi (a)\varphi (b)=\varphi (ab)=\tilde{\varphi }([ab])=\tilde{\varphi }([a][b])$. As stated already, $\tilde{\varphi }([a])=\varphi (a)$ shows uniqueness, proving the theorem. Template:Unicode

Lemma 13: Let $\sim$ be an equivalence relation on a group $G$ such that $a\sim b\iff ga\sim gb$. Then $H=[e]$ is a subgroup of $G$ and $a\sim b\iff a^{-1}b\in H\iff aH=bH$.

Proof: First off, $H$ is nonempty since $e\in H$. Let $a,b\in H$. Then $b\sim e\iff e\sim b^{-1}$ by multiplying on the left by $b^{-1}$. Then since $e\sim a$ we have $a^{-1}\sim e$ by the same argument. Applying transitivity gives $a^{-1}\sim b^{-1}$. Finally, multiplying on the left by $a$ gives $e\sim a{b}^{-1}$, giving $a{b}^{-1}\in H$ and so $H=[e]$ is a subgroup.

Assume $a\sim b$ for $a,b\in G$. Then $[a]=[b]$ implying $[a^{-1}b]=[e]$. Thus $a^{-1}b\in [e]$. Now assume $a^{-1}b\in [e]$. Then $[a^{-1}b]=[e]$ and so $[a]=[b]$ and finally $a\sim b$.

Assume $a^{-1}b\in H$. Then since $H$ is a subgroup, we have $a^{-1}bH=H$ and so $aH=bH$. Finally, assume $aH=bH$. Then $a^{-1}bH=H$. Since in particular $e\in H$, this implies $a^{-1}b\in H$, completing the proof. Template:Unicode

The mirror version using right cosets and the equivalence relation $a\sim b\iff ag\sim bg$ and $a\sim b\iff a{b}^{-1}\in H\iff Ha=Hb$ is completely analogous. Stating the theorem and writing out the proof is left to the reader as an exercise.

We have showed how an equivalence relation defines a subgroup of $G$. In fact the equivalence classes are all cosets of this subgroup. We will now go the other way, and show how a subgroup defines an equivalence relation on $G$.

Lemma 14: Let $H$ be a subgroup of a group $G$. Then,

i) $a{\sim }_{L}b\iff a^{-1}b\in H\iff aH=bH$ is an equivalence relation such that $a{\sim }_{L}b\iff ga{\sim }_{L}gb$ for all $g\in G$.

ii) $a{\sim }_{R}b\iff a{b}^{-1}\in H\iff Ha=Hb$ is an equivalence relation such that $a{\sim }_{R}b\iff ag{\sim }_{R}bg$ for all $g\in G$.

Proof: We will prove i). The proof for ii) is similar and is left as an exercise for the reader.

The fact that $\sim$ is an equivalence relation and that $a^{-1}b\in H\iff aH=bH$ was proven in the section on subgroups. Assume $a{\sim }_{L}b$. Then for all $g\in G$, $(ga{)}^{-1}(gb)=a^{-1}{g}^{-1}gb=a^{-1}b\in H$ such that $ga{\sim }_{L}gb$. Now assume $ga{\sim }_{L}gb$, Then $a^{-1}b=a^{-1}{g}^{-1}gb=(ga{)}^{-1}(gb)\in H$ such that $a{\sim }_{L}b$, completing the proof. Template:Unicode

Theorem 15: For every equivalence relation ${\sim }_L$ on G such that $a{\sim }_{L}b\iff ga{\sim }_{L}gb$, there exists a unique subgroup $H$ of $G$ such that $G/\sim$ are precisely the left cosets of $H$.

Proof: This follows from Lemma 13 and Lemma 14.

Again, the mirror statement is completely analogous. Stating the theorem is left to the reader as an exercise.

Quotients with respect to Normal Subgroups

Lemma 16: Let ${\sim }_L$ be the equivalence relation given by $a{\sim }_{L}b:\iff aH=bH$, where $H$ is a subgroup of G. Then we know that ${\sim }_L$ is compatible if and only if $H$ is a normal subgroup.

Proof: Assume ${\sim }_L$ is compatible, $g\in G$ and $a\in H$. Then $a{\sim }_{L}e$, and compatibility gives us $ga{g}^{-1}{\sim }_{L}g{g}^{-1}=e$, and so $ga{g}^{-1}\in H$. Since $a$ is arbitrary, we obtain $gH{g}^{-1}=H$ for all $g\in G$ and so $H$ is normal. Assume now that $H$ is normal. Then $aH=bH\iff a^{-1}b\in H$, $Ha=Hb\iff a{b}^{-1}\in H$ and $aH=Ha$ for all $a,b\in G$. Using this, we obtain $a{\sim }_{L}b\iff a{b}^{-1}=a{b}^{-1}bg(bg{)}^{-1}{\sim }_{L}e\iff a{b}^{-1}bg=ag{\sim }_{L}bg$ and similarly for the right hand case, so ${\sim }_L$ is compatible with $G$. Template:Unicode

Definition 17: When an equivalence relation is given by specifying a normal subgroup $H$, the quotient group with respect to this equivalence relation is denoted $G/H$. We then refer to $G/H$ as the quotient of $G$ with respect to $H$, or $G$ modulo $H$. Note that this complies with previous definitions of this notation.

Multiplication in $G/H$ is given as before as $(aH)(bH)=(ab)H$, with identity $H$ and $(aH{)}^{-1}=a^{-1}H$ for all $a,b\in G$.

Definition 18: Let $H$ be a normal subgroup of $G$. Then we define the projection homomorphism $\pi :G\to G/H$ by $\pi (a)=aH$ for all $a\in G$.

Theorem 19: A subgroup is normal if and only if it is the kernel of some homomorphism.

Proof: We have already covered the left implication. For the right implication, assume $H$ is normal. Then $G/H$ is a group and we have the projection homomorphism $\pi :G\to G/H$ as defined above. Since for all $h\in H$ we have $\pi (h)=hH=H$, $\ker \pi =H$ and so $H$ is the kernel of a homomorphism. Template:Unicode

Theorem 20: Let $G,G^{\prime }$ be groups, $\varphi :G\to G^{\prime }$ a homomorphism and $H$ a normal subgroup of $G$ such that $H\subseteq \ker \varphi$. Then there exists a unique homomorphism $\tilde{\varphi }:G/H\to G^{\prime }$ such that $\tilde{\varphi }\circ \pi =\varphi$.

Proof: This follows from Theorem 12 by letting $a\sim b\iff aH=bH$. Template:Unicode

The Isomorphism Theorems

Commutative diagram showing the first isomorphism theorem. $\tilde{\varphi }$ is an isomorphism.

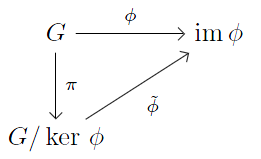
Theorem 21 (First Isomorphism Theorem): Let $G,G^{\prime }$ be groups and $\varphi :G\to G^{\prime }$ a homomorphism. Then $G/\ker \varphi \approx \mathrm{i}\mathrm{m}\varphi$.

Proof: From Theorem 20 we have that there exists a unique homomorphism $\tilde{\varphi }:G/\ker \varphi \to G^{\prime }$ such that $\varphi =\tilde{\varphi }\circ \pi$. We have to show that $\tilde{\varphi }$ is an isomorphism when we corestrict to $\mathrm{i}\mathrm{m}\varphi$. This is immediate, since $\varphi (a)=\varphi (b)\iff a\ker \varphi =b\ker \varphi$ by Lemma 13, so that $\tilde{\varphi }$ is injective, and for any $g^{\prime }\in \mathrm{i}\mathrm{m}\varphi$ there is a $g\in G$ such that $\varphi (g)=\tilde{\varphi }(g\ker \varphi )=g^{\prime }$ so that it is surjective and therefore an isomorphism. Template:Unicode

Lemma 22: Let $G$ be a group, $H$ a subgroup and $K$ a normal subgroup of $G$. Then $H\cap K$ is a normal subgroup of $H$.

Proof: Let $h\in H$ and $k\in H\cap K$. Then $hk{h}^{-1}\in H$ since $h,k\in H$ and $H$ is a subgroup and $hk{h}^{-1}\in K$ since $k\in K$, $h\in G$ and $K$ is normal in $G$. Thus $hk{h}^{-1}\in H\cap K$ and $H\cap K$ is normal in $H$. Template:Unicode

Theorem 23 (Second Isomorphism Theorem): Let $G$ be a group, $H$ a subgroup and $K$ a normal subgroup of $G$. Then $HK/K\approx \frac{H}{H\cap K}$.

Proof: Define $\varphi :H\to HK/K$ by $\varphi (h)=hK$ for all $h\in H$. $\varphi$ is surjective since any element in $HK$ can be written as $hk$ with $h\in H$ and $k\in K$, so $\varphi (h)=\pi (hk)=hkK=hK$. We also have that $\ker \varphi =\{h\in H\mid hK=K\}=\{h\in H\mid h\in K\}=H\cap K$ and so $HK/K\approx \frac{H}{H\cap K}$ by the first isomorphism theorem. Template:Unicode

Lemma 24: Let $G$ be a group, and let $H,K$ be normal subgroups of $G$ such that $K\subseteq H\subseteq G$. Then $H/K$ is a normal subgroup of $G/K$.

Proof: Let $h\in H$ and $g\in G$. Then $gh{g}^{-1}=h^{\prime }$ for some $h^{\prime }\in H$ since $H$ is normal. Thus $(gK)(hK)(gK{)}^{-1}=(gh{g}^{-1})K=h^{\prime }K$, showing that $H/K$ is normal in $G/K$. Template:Unicode

Theorem 25 (Third Isomorphism Theorem) Let $G$ be a group, and let $H,K$ be normal subgroups of $G$ such that $K\subseteq H\subseteq G$. Then $\frac{G/K}{H/K}\approx G/H$.

Proof: Let $\varphi :G/K\to G/H$ be given by $\varphi (gK)=gH$. This is well defined and surjective since $K\subseteq H$, and is a homomorphism. Its kernel is given by $\ker \varphi =\{gK\in G/K\mid gH=H\}=\{gK\in G/K\mid g\in H\}=H/K$, so by the first isomorphism theorem, $\frac{G/K}{H/K}\approx G/H$. Template:Unicode

Theorem 26 (The Correspondence Theorem): Let $G$ be a group and $K$ be a normal subgroup. Now let $A=\{H\le G\mid K\le H\}$ and $B=\{H^{\prime }\mid H^{\prime }\le G/K\}$. Then $\pi :H\mapsto \pi (H)$ is an order-preserving bijection from $A$ to $B$.

Proof: We must show injectivity and surjectivity. For injectivity, note that if $K\le H$, then ${\pi }^{-1}(\pi (H))=HK=H$, so if $H_1,H_2\in A$ such that $\pi (H_1)=\pi (H_2)$, then $H_1={\pi }^{-1}(\pi (H_1))={\pi }^{-1}(\pi (H_2))=H_2$, proving injectivity. For surjectivity, let $H^{\prime }\in B$. Then $K\le {\pi }^{-1}(H^{\prime })\le G$, so that ${\pi }^{-1}(H^{\prime })\in A$, and $\pi ({\pi }^{-1}(H^{\prime }))=H^{\prime }$, proving surjectivity. Lastly, since $H_1\subseteq H_2$ implies that $\pi (H_1)\subseteq \pi (H_2)$, the bijection is order-preserving. Template:Unicode

Note 27: The correspondence Theorem is sometimes called The Forth Isomorphism Theorem.

Theorem 28: Let $H\in A$ from Theorem 26. Then $H$ is normal if and only if $\pi (H)$ is normal in $G/K$, and then $G/H\approx \frac{G/K}{\pi (H)}$.

Proof: Since $\pi$ is surjective, $H$ normal implies $\pi (H)$ normal. Assume that $\pi (H)$ is normal. Then ${\pi }^{-1}(\pi (H))=H$ and so $H$ is normal since it is the preimage of a normal subgroup. To show the isomorphism, let $\varphi :G\to \frac{G/K}{\pi (H)}$ be given by a composition of projections: $\varphi :{\pi }_{\pi (H)}\circ {\pi }_K$. Then $\ker \varphi =\{g\in G\mid \varphi (g)=\pi (H)\}=\{g\in G\mid \pi (g)\in \pi (H)\}={\pi }^{-1}(\pi (H))=H$, so by the first isomorphism teorem, $G/H\approx \frac{G/K}{\pi (H)}$. Template:Unicode

Corollary 29: Let $G$ be a group and $H$ a normal subgroup. Then for any $K^{\prime }\le G/H$ there exists a unique subgroup $K\le G$ such that $H\le K\le G$ and $K=K^{\prime }H$. Also, $K$ is normal in $G$ if and only if $K^{\prime }$ is normal in $G/H$.

Proof: From Theorem 26 we have that the projection $K\mapsto \pi (K)=K^{\prime }$ is a bijection, and since $\pi (g)=gH$ for all $g\in G$, we have $K=K^{\prime }H$. The second part follows from Theorem 28. Template:Unicode

Proof:

Due to theorem 2.6.?, $HI$ and $KI$ are subgroups of $G$. Further, theorem 2.6.? implies that $KI⊴HI$. Therefore, the function

$\mathrm{\Phi }:H\to HI/KI,\mathrm{\Phi }(h):=hKI$

is a homomorphism.

Further, since $K$ is a subgroup of $H$, for all $h=\kappa \iota \in KI,\kappa \in K,\iota \in I$ we have:

$h\in H\Rightarrow {\kappa }^{-1}h=\iota \in H$

And thus:

$\begin{array}{cc}h\in \ker \mathrm{\Phi }& \iff h=\kappa \iota ,\kappa \in K,\iota \in I\\ & \iff h=\kappa \iota ,\kappa \in K,\iota \in H\cap I\\ & \iff h\in K(H\cap I)\end{array}$

Therefore, $\ker \mathrm{\Phi }=K(H\cap I)$. Thus, the first isomorphism theorem implies

$HI/KI\cong H/(K(H\cap I))$ $◻$

Simple Groups

Definition 30: A group is called simple if it has no non-trivial proper normal subgroups.

Example 31: Every cyclic group ${\mathbb{Z}}_p$, where $p$ is prime, is simple.

Definition 32: Let $G$ be a group and $H$ a normal subgroup. $H$ is called a maximal normal subgroup if for any normal subgroup $K$ of $G$, we have $K\subseteq H$.

Theorem 33: Let $G$ be a group and $H$ a normal subgroup. Then $H$ is a maximal normal subgroup if and only if the quotient $G/H$ is simple.

Proof: By Theorem 26 and Theorem 28, $G/H$ has a nontrivial normal subgroup if and only if there exists a proper normal subgroup $K$ of $G$ such that $H\le K\le G$. That is, $H$ is not maximal if and only if $G/H$ is not simple. The theorem follows. Template:Unicode

Problems

Problem 1: Recall the unitary and special unitary groups from the section about subgroups. Define the projective unitary group of order $n$ as the group $PU(n)=U(n)/Z(U(n))$. Similarly, define the projective special unitary group of order $n$ as $PSU(n)=SU(n)/Z(SU(n))$.

i) Show that $Z(SU(n))=SU(n)\cap Z(U(n)\approx {\mathbb{Z}}_n$

ii) Using the second isomorphism theorem, show that $PSU(n)\approx PU(n)$.