Topology/Vector Spaces

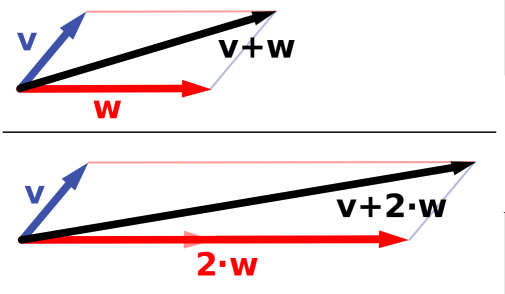
A vector space $V$ is formed by scalar multiples of vectors. The scalars are most commonly real numbers but can also be complex, or from any field.

Definition

A vector space $V$ on a field $F$ is a set $V$ equipped with two binary operations: common vector addition on elements of $V$ and scalar multiplication, by elements of $F$ on elements of $V$. These operations are subject to 8 axioms (u,v, and w are vectors in $V$ and a and b are scalars in $F$):

1. Associativity (addition): (u+v)+w = u+(v+w).

2. Associativity (scalar and field multiplication): a(bu) = (ab)u

3. Distributivity (field addition): (a+b)u = au+bu

4. Distributivity (vector addition): a(u+v) = au+av

5. Identity element (addition): $\mathrm{\exists }$ 0 $\in V$ such that u+0 = u $\mathrm{\forall }$ u $\in V$

6. Identity element (scalar multiplication): 1u = u

7. Commutativity: u+v = v+u

8. Inverse element: $\mathrm{\exists }$ -u $\in V$ such that u+(-u) = 0 $\mathrm{\forall }$ u $\in V$

An example of basic arrow vectors: first the black vector as the sum of the red and blue vectors, then the black vector as a sum of the blue vector and a scaling of the red vector (x2)

Template:Navigation