Commutative Algebra/Irreducibility, algebraic sets and varieties

Irreducibility

Some people (topologists) call irreducible spaces hyperconnected.

Proof 1: We prove 1. $\Rightarrow$ 2. $\Rightarrow$ 3. $\Rightarrow$ 4. $\Rightarrow$ 1.

1. $\Rightarrow$ 2.: Assume that $X=A\cup B$, where $A$, $B$ are proper and closed. Define $O:=X\setminus A$ and $U:=X\setminus B$. Then $O,U$ are open and

$O\cap U=(X\setminus A)\cap (X\setminus B)=X\setminus (A\cup B)=\mathrm{\varnothing }$

by one of deMorgan's rules, contradicting 1.

2. $\Rightarrow$ 3.: Assume that $U\subseteq X$ is open but not dense. Then $A:=\bar{U}$ is closed and proper in $X$, and so is $B:=X\setminus U$. Furthermore, $X=A\cup B$, contradicting 2.

3. $\Rightarrow$ 4.: Let $\mathrm{\varnothing }\ne A⊊X$ be closed such that $\stackrel{\circ }{A}\ne \mathrm{\varnothing }$. By definition of the closure, $\overline{\stackrel{\circ }{A}}\subseteq A$, which is why $\stackrel{\circ }{A}$ is a non-dense open set, contradicting 3.

4. $\Rightarrow$ 1.: Let $O,U\subseteq X$ be open and non-empty such that $O\cap U=\mathrm{\varnothing }$. Define $A:=X\setminus O$. Then $A$ is a proper, closed subset of $X$, since $O\subseteq X\setminus A$. Furthermore, $O\subseteq \stackrel{\circ }{A}$, which is why $A$ has non-empty interior.$◻$

Proof 2: We prove 1. $\Rightarrow$ 4. $\Rightarrow$ 3. $\Rightarrow$ 2. $\Rightarrow$ 1.

1. $\Rightarrow$ 4.: Assume we have a proper closed subset $A$ of $X$ with nonempty interior. Then $X\setminus A$ and $\stackrel{\circ }{A}$ are two disjoint nonempty open subsets of $X$.

4. $\Rightarrow$ 3.: Let $O\subseteq X$ be open. If $O$ was not dense in $X$, then $\bar{O}$ would be a proper closed subset of $X$ with nonempty interior.

3. $\Rightarrow$ 2.: Assume $X=A\cup B$, $A,B⊊X$ proper and closed. Set $O:=X\setminus B$. Then $A\supset O$, and hence $O$ is not dense within $X$.

2. $\Rightarrow$ 1.: Let $O,U\subseteq X$ be open. If they are disjoint, then $X=(X\setminus O)\cup (X\setminus U)$.$◻$

Remaining arrows:

1. $\Rightarrow$ 3.: Assume $U\subset X$ open, not dense. Then $X\setminus \bar{U}$ is nonempty and disjoint from $U$.

3. $\Rightarrow$ 1.: Let $O,U\subseteq X$ be open. If they are disjoint, then $O\subseteq X\setminus U$ and thus $O$ is not dense.

2. $\Rightarrow$ 4.: Let $A⊊X$ be proper and closed with nonempty interior. Then $X=A\cup (X\setminus \stackrel{\circ }{A})$.

4. $\Rightarrow$ 2.: Let $X=A\cup B$, $A,B⊊X$ proper and closed. Then $\mathrm{\varnothing }\ne X\setminus A\subseteq \stackrel{\circ }{A}$.

We shall go on to prove a couple of properties of irreducible spaces.

Theorem 21.3:

Every irreducible space $X$ is connected and locally connected.

Proof:

1. Connectedness: Assume $X=U\dot{\cup }O$, $U,O$ open, non-empty. This certainly contradicts irreducibility.

2. Local connectedness: Let $x\in V\subseteq X$, where $V$ is open. But any open subset of $X$ is connected as in 1., which is why we have local connectedness.$◻$

Theorem 21.4:

Let $X$ be an irreducible space. Then $X$ is Hausdorff if and only if $|X|\le 1$.

Proof:

If $|X|\le 1$, then $X$ is trivially Hausdorff. Assume that $X$ is Hausdorff and contains two distinct points $x\ne y$. Then we find $U_x,U_y\subseteq X$ open such that $x\in U_x$, $y\in U_y$ and $U_x\cap U_y=\mathrm{\varnothing }$, contradicting irreducibility.$◻$

Theorem 21.5:

Let $X,Y$ be topological spaces, where $X$ is irreducible, and let $f:X\to Y$ be a continuous function (i.e. a morphism in the category of topological spaces). Then $f(X)$ is irreducible with the subspace topology induced by $Y$.

Proof: Let $O,U$ be two disjoint non-empty open subsets of $f(X)$. Since we are working with the subspace topology, we may write $O=f(X)\cap V$, $U=f(X)\cap W$, where $V,W\subseteq Y$ are open. We have

$f^{-1}(O)=f^{-1}(f(X)\cap V)=f^{-1}(V)$ and similarly $f^{-1}(U)=f^{-1}(W)$.

Hence, $f^{-1}(O)$ and $f^{-1}(U)$ are open in $X$ by continuity, and since they further are disjoint (since if $x\in f^{-1}(O)$, then $f(x)\in O$ and thus $f(x)\notin U$) and non-empty (since e.g. if $y\in O$, since $O\subset f(X)$, $y=f(x)$ for an $x\in X$ and hence $x\in f^{-1}(O)$), we have a contradiction.$◻$

Corollary 21.6:

If $X$ is irreducible, $Y$ is Hausdorff and $f:X\to Y$ is continuous, then $f$ is constant.

Proof: Follows from theorems 21.4 and 21.5.$◻$

We may now connect irreducible spaces with Noetherian spaces.

Proof:

First we prove existence. Let $A\subseteq X$ be closed. Then either $A$ is irreducible, and we are done, or $A$ can be written as the union of two proper closed subsets $A=B_1\cup B_2$. Now again either $B_1$ and $B_2$ are irreducible, or they can be written as the union of two proper closed subsets again. The process of thus splitting up the sets must eventually terminate with all involved subsets being irreducible, since $X$ is Noetherian and otherwise we would have an infinite properly descending chain of closed subsets, contradiction. To get the last condition satisfied, we unite any subset contained within another with the greater subset (this can be done successively since there are only finitely many of them). Hence, we have a decomposition of the desired form.

We proceed to proving uniqueness up to order. Let $A=B_1\cup \cdots \cup B_n=C_1\cup \cdots \cup C_m$ be two such decompositions. For $k\in \{1,\dots ,n\}$, we may thus write $B_k=(B_k\cap C_1)\cup \cdots \cup (B_k\cap C_m)$. Assume that there does not exist $j\in \{1,\dots ,m\}$ such that $B_k\subseteq C_j\iff B_k=(B_k\cap C_j)$. Then we may define $S_1:=(B_k\cap C_1)$ and then successively

$S_{l+1}:=S_l\cup (B_k\cap C_{l+1})$

for $1\le l<m$. Then we set $l=1$ and increase $l$ until $S_l\cup (B_k\cap C_{l+1})$ is a decomposition of $B_k$ into two proper closed subsets (such an $l$ exists since it equals the first $l$ such that $S_l\cup (B_k\cap C_{l+1})=B_k$). Thus, our assumption was false; there does exist $j\in \{1,\dots ,m\}$ such that $B_k\subseteq C_j$. Thus, each $B_k$ is contained within a $C_j$, and by symmetry $C_j$ is contained within some $B_{k^{\prime }}$. Since by transitivity of $\subseteq$ this implies $B_k\subseteq B_{k^{\prime }}$, $k=k^{\prime }$ and $C_j=B_k$. For a fixed $k$, we set $\sigma (k)=j$, where $j$ is thus defined ($j$ is unique since otherwise there exist two equals among the $C$-sets). In a symmetric fashion, we may define $\tau (j)=k$, where $B_k=C_j$. Then $\tau$ and $\sigma$ are inverse to each other, and hence follows $n=m$ (sets with a bijection between them have equal cardinality) and the definition of $\sigma$, for example, implies that both decompositions are equal except for order.$◻$

Exercises

• Exercise 21.1.1: Let $X$ be an irreducible topological space, and let $O\subseteq X$ be open. Prove that $O$ is irreducible.

Algebraic sets and varieties

The following picture depicts three algebraic sets (apart from the cube lines):

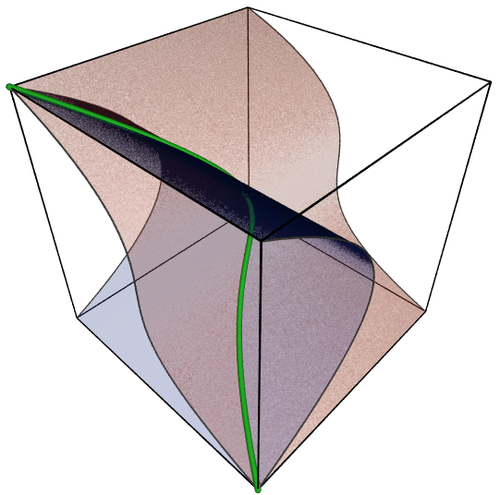
The orange surface is the set $V(f_1)$, the blue surface is the set $V(f_2)$, and the green line is the intersection of the two, equal to the set $V(\{f_1,f_2\})$, where

$f_1(x,y,z)=z+y^3$ and

$f_2(x,y,z)=x+z^2$.

Three immediate lemmata are apparent.

Lemma 21.9:

$S\subseteq T\Rightarrow V(T)\subseteq V(S)$.

Proof: Being in $V(T)$ is the stronger condition.$◻$

Lemma 21.10 (formulas for algebraic sets):

Let $𝔽$ be a field and set $R:=𝔽[x_1,\dots ,x_n]$. Then the following rules hold for algebraic sets of ${𝔽}^n$:

1. $V(S)=V(⟨S⟩)$ ($S\subseteq R$ a set)
2. $V(R)=\mathrm{\varnothing }$ and $V(\mathrm{\varnothing })={𝔽}^n$
3. $V(I_1)\cup \cdots \cup V(I_k)=V(I_1\cap \cdots \cap I_k)$ ($I_1,\dots ,I_k\le R$ ideals)
4. $\bigcap _{j\in J}V(S_j)=V\left(\bigcup _{j\in J}{S}_j\right)$ ($S_j\subseteq R$ sets)

Proof:

1. Let $i:=\sum _{j=1}^k{r}_j{s}_j\in ⟨S⟩$. If $x=(x_1,\dots ,x_n)\in V(S)$ follows $i(x)=0$. This proves $\subseteq$. The other direction follows from lemma 21.9.

2. $V(R)=\mathrm{\varnothing }$ follows from the constant functions being contained within $R$, and $V(\mathrm{\varnothing })$ gives no condition on the points of ${𝔽}^n$ to be contained within it.

3. $\subseteq$ follows by

$\begin{array}{cc}x\in V(I_1)\cup \cdots \cup V(I_k)& \Rightarrow \mathrm{\exists }j\in \{1,\dots ,k\}:x\in V(I_j)\\ & \Rightarrow \mathrm{\forall }f\in I_j:f(x)=0\\ & \Rightarrow \mathrm{\forall }f\in I_1\cap \cdots \cap I_k:f(x)=0,\end{array}$

since clearly $I_1\cap \cdots \cap I_k\subseteq I_j$.

We will first prove $\supseteq$ for the case $k=2$. Indeed, let $x\notin V(I_1)\cup V(I_2)$, that is, neither $x\in V(I_1)$ nor $x\in V(I_2)$. Hence, we find a polynomial $f\in I_1$ such that $f(x)\ne 0$ and a polynomial $g\in S_2$ such that $g(x)\ne 0$. The polynomial $f\cdot g$ is contained within $I_1\cap I_2$ and $(f\cdot g)(x)=f(x)\cdot g(x)\ne 0$, since every field is an integral domain. Thus, $x\notin V(I_1\cap I_2)$.

Assume $\supseteq$ holds for $k-1$ many sets. Then we have

$V(I_1\cap \cdots \cap I_k)=V((I_1\cap \cdots I_{k-1})\cap I_k)\subseteq V(I_1\cap \cdots I_{k-1})\cup V(I_k)\subseteq V_{(}{I}_1)\cup \cdots \cup V(I_{k-1})\cup V(I_k)$.

4.

$\begin{array}{cc}x\in \bigcap _{j\in J}V(S_j)& \iff \mathrm{\forall }j\in J:x\in V(S_j)\\ & \iff \mathrm{\forall }j\in J:\mathrm{\forall }f\in S_j:f(x)=0\\ & \iff \mathrm{\forall }f\in \bigcup _{j\in J}{S}_j:f(x)=0\\ & \iff x\in V\left(\bigcup _{j\in J}{S}_j\right).\end{array}$$◻$

From this lemma we see that the algebraic sets form the closed sets of a topology, much like the Zariski-closed sets we got to know in chapter 14. We shall soon find a name for that topology, but we shall first define it in a different way to justify the name we will give.

Lemma 21.11:

Let $𝔽$ be a field and $I\subseteq 𝔽[x_1,\dots ,x_n]$. Then

$V(I)=V(r(I))$;

we recall that $r(I)$ is the radical of $I$.

Proof: "$\supseteq$" follows from lemma 21.9. Let on the other hand $x\in V(I)$ and $g\in r(I)$. Then $g^k\in I$ for a suitable $k\in \mathbb{N}$. Thus, $g^k(x)=g(x{)}^k=0$. Assume $g(x)\ne 0$. Then $g(x{)}^k\ne 0$, contradiction. Hence, $x\in V(r(I))$.$◻$

From calculus, we all know that there is a natural topology on ${ℝ}^n$, namely the one induced by the Euclidean norm. However, there exists also a different topology on ${ℝ}^n$, and in fact, on ${𝔽}^n$ for any field $𝔽$. This topology is called the Zariski topology on ${𝔽}^n$. Now the Zariski topology actually is a topology on $\mathrm{Spec}R$, for $R$ a ring, isn't it? Yes, and if $R=𝔽[x_1,\dots ,x_n]$, then ${𝔽}^n$ is in bijective correspondence with a subset of $\mathrm{Spec}R$. Through this correspondence we will define the Zariski topology. So let's establish this correspondence by beginning with the following lemma.

Lemma 21.12:

Let $𝔽$ be a field and set $R:=𝔽[x_1,\dots ,x_n]$. If $({\alpha }_1,\dots ,{\alpha }_n)\in {𝔽}^n$, then the ideal

$⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$

is a maximal ideal of $R$.

Proof:

Set

$\phi :𝔽[x_1,\dots ,x_n]\to 𝔽,\phi (f):=f({\alpha }_1,\dots ,{\alpha }_n)$.

This is a surjective ring homomorphism. We claim that its kernel is given by $⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$. This is actually not trivial and requires explanation. The relation $⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩\subseteq \ker \phi$ is trivial. We shall now prove the other direction, which isn't. For a given $f\in 𝔽[x_1,\dots ,x_n]$, we define $\tilde{f}(x_1,x_2,\dots ,x_n):=f(x_1+{\alpha }_1,\dots ,x_n+{\alpha }_n)$; hence,

$\begin{array}{cc}f(x_1,x_2,\dots ,x_n)& =f(x_1+{\alpha }_1-{\alpha }_1,\dots ,x_n+{\alpha }_n-{\alpha }_n)\\ & =\tilde{f}(x_1-{\alpha }_1,x_2-{\alpha }_2,\dots ,x_n-{\alpha }_n).\end{array}$

Furthermore, $f({\alpha }_1,\dots ,{\alpha }_n)=0$ if and only if $\tilde{f}(0,\dots ,0)=0$. The latter condition is satisfied if and only if $\tilde{f}$ has no constant, and this happens if and only if $\tilde{f}$ is contained within the ideal $⟨x_1,\dots ,x_n⟩$. This means we can write $\tilde{f}$ as an $𝔽[x_1,\dots ,x_n]$-linear combination of $x_1,\dots ,x_n$, and inserting $x_j-{\alpha }_j$ for $x_j$ gives the desired statement.

Hence, by the first isomorphism theorem for rings,

$𝔽[x_1,\dots ,x_n]/⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩\cong 𝔽$.

Thus, $𝔽[x_1,\dots ,x_n]/⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$ is a field and hence $⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$ is maximal.$◻$

Lemma 21.13:

Let $𝔽$ be a field. Define

${ℳ}_{𝔽}:=\{⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩|({\alpha }_1,\dots ,{\alpha }_n)\in {𝔽}^n\}$

(according to the previous lemma this is a subset of $\mathrm{Spec}𝔽[x_1,\dots ,x_n]$, as maximal ideals are prime). Then the function

$\mathrm{\Phi }:{𝔽}^n\to {ℳ}_{𝔽},f(({\alpha }_1,\dots ,{\alpha }_n)):=⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$

is a bijection.

Proof:

The function is certainly surjective. Let $⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩=⟨x_1-{\beta }_1,\dots ,x_n-{\beta }_n⟩$, and assume ${\beta }_j\ne {\alpha }_j$ for a certain $j\in \{1,\dots ,n\}$. Then $x_j-{\beta }_j\in ⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$, and thus

$0\ne {\alpha }_j-{\beta }_j=x_j-{\beta }_j-(x_j-{\alpha }_j)\in ⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$.

Thus, $⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩$ contains a unit and therefore equals $𝔽[x_1,\dots ,x_n]$, contradicting its maximality that was established in the last lemma.$◻$

It is easy to check that the sets ${\mathrm{\Phi }}^{-1}(O)$, $O\subseteq {ℳ}_{𝔽}$ really do form a topology.

There is a very simple different way to characterise the Zariski topology:

Proof:

Unfortunately, for a set $T\subseteq 𝔽[x_1,\dots ,x_n]$, the notation $V(T)$ is now ambiguous; it could refer to the algebraic set associated to $T$, or to the set of prime ideals $p$ of $𝔽[x_1,\dots ,x_n]$ satisfying $T\subseteq p$. Hence, we shall write the latter as $\tilde{V}(T)$ for the remainder of this wikibook.

Let $A\subseteq {𝔽}^n$ be closed w.r.t. the Zariski topology; that is, $A={\mathrm{\Phi }}^{-1}(\tilde{V}(T)\cap {ℳ}_{𝔽})$, where $\mathrm{\Phi }$ is the function from lemma 21.13 and $T\subseteq R:=𝔽[x_1,\dots ,x_n]$. We claim that $A=V(T)$. Indeed, for $\alpha \in {𝔽}^n$,

$\begin{array}{cc}\alpha \in V(T)& \iff \mathrm{\forall }f\in T:f(\alpha )=0\\ & \iff \mathrm{\forall }f\in T:((x_1-{\alpha }_1)|f\vee \cdots \vee (x_1-{\alpha }_1)|f)\\ & \iff \mathrm{\forall }f\in T:f\in ⟨x_1-{\alpha }_1,\dots ,x_n-{\alpha }_n⟩\\ & \iff T\subseteq \mathrm{\Phi }(\alpha )\\ & \iff \mathrm{\Phi }(\alpha )\in \tilde{V}(T)\\ & \iff \alpha \in {\mathrm{\Phi }}^{-1}(\tilde{V}(T)\cap {ℳ}_{𝔽})\end{array}$.

Let now $V(S)$ be an algebraic set. We claim $V(S)={\mathrm{\Phi }}^{-1}(\tilde{V}(S)\cap {ℳ}_{𝔽})$. Indeed, the above equivalences prove also this identity (with $S$ replacing $T$).$◻$

In fact, we could have defined the Zariski topology in this way (that is, just defining the closed sets to be the algebraic sets), but then we would have hidden the connection to the Zariski topology we already knew.

We shall now go on to give the next important definition, which also shows why we dealt with irreducible spaces.

Often, we shall just write variety for algebraic variety.

We have an easy characterisation of algebraic varieties. But in order to prove it, we need a definition with theorem first.

Proof:

Let first $T$ be any set such that $V(T)=V(S)$. Then for all $f\in T$ and $x\in V(S)=V(T)$, $f(x)=0$ and hence $f\in I(V(S))$. Thus $T\subseteq I(V(S))$.

Therefore, $S\subseteq I(V(S))$, and hence $V(I(V(S)))\subseteq V(S)$ by lemma 21.9. On the other hand, if $x\in V(S)$, then $f(x)=0$ for all $f\in I(V(S))$ by definition. Hence $x\in V(I(V(S)))$. This proves $V(S)\subseteq V(I(V(S)))$.$◻$

Proof:

Let first $p\le 𝔽[x_1,\dots ,x_n]$ be a prime ideal. Assume that $V(p)=V(S)\cup V(T)$, where $V(S),V(T)$ are two proper closed subsets of $V(p)$ (according to lemma 21.10, all subsets of $V(p)$ closed w.r.t. the subspace topology of $V(p)$ have this form). Then there exist $x\in V(p)\setminus V(T)$ and $y\in V(p)\setminus V(S)$. Hence, there is $g\in T$ such that $g(x)\ne 0$ and $f\in S$ such that $f(y)\ne 0$. Furthermore, $f\cdot g\in p$ since for all $z\in V(S)\cup V(T)$ either $f(z)=0$ or $g(z)=0$, but neither $f\in p$ nor $g\in p$.

Let now $V(S)$ be an algebraic set, and assume that $I:=I(V(S))$ is not prime. Let $fg\in I$ such that neither $f\in I$ nor $g\in I$. Set $J_f:=I+⟨f⟩$ and $J_g:=I+⟨g⟩$. Then $J_f$ and $J_g$ are strictly larger than $I$. According to 21.17, $V(J_f)\ne V(S)$ and $V(J_g)\ne V(S)$, since otherwise $J_f\subseteq I$ or $J_g\subseteq I$ respectively. Hence, both $V(J_f)$ and $V(J_g)$ are proper subsets of $V(S)$. But if $x\in V(S)=V(I)$, then $fg(x)=f(x)g(x)=0$. Hence, either $f(x)=0$ or $g(x)=0$, and thus either $x\in J_f$ or $x\in J_g$. Thus, $V(S)$ is the union of two proper closed subsets,

$V(S)=V(J_g)\cup V(J_f)$,

and is not irreducible. Hence, if irreducibility is present, then $I(V(S))$ is prime and from 21.17 $V(I(V(S)))=V(S)$.$◻$

Proof:

Let $O_1\subseteq O_2\subseteq \cdots \subseteq O_k\subseteq \cdots$ be an ascending chain of open sets. Let $\mathrm{\Phi }$ and ${ℳ}_{𝔽}$ be given as in lemma 21.13 and definition 21.14. Set $U_j=\mathrm{\Phi }(O_j)$ for all $j\in \mathbb{N}$. Then, since $\mathrm{\Phi }$, being a function, preserves inclusion,

$U_1\subseteq U_2\subseteq \cdots \subseteq U_k\subseteq \cdots$.

Since $𝔽$ is a Noetherian ring, so is $𝔽[x_1,\dots ,x_n]$ (by repeated application of Hilbert's basis theorem). Hence, the above ascending chain of the $U_j$ eventually stabilizes at some $N\in \mathbb{N}$. Since $\mathrm{\Phi }$ is a bijection, $O_j={\mathrm{\Phi }}^{-1}(\mathrm{\Phi }(O_j))={\mathrm{\Phi }}^{-1}(U_j)$. Hence, the $O_j$ stabilize at $N$ as well.$◻$

That is, we can decompose algebraic sets into algebraic varieties.

Proof:

Combine theorems 21.19, 21.7 and 21.18.$◻$

Exercises

• Exercise 21.2.1: Let $f,g\in 𝔽[x_1,\dots ,x_n]$. Prove that $V(\{f\cdot g\})=V(\{f\})\cup V(\{g\})$.