Analytic Combinatorics/Meromorphic Functions

Introduction

This article explains how to estimate the coefficients of meromorphic generating functions which have only one dominant singularity.

Theorem

Theorem due to Sedgewick.

• If $h(z)=\frac{f(z)}{g(z)}$ is a meromorphic function
• which has only one pole, $a$, closest to the origin, with order $m$
• then you can estimate its $n$th coefficient with the formula:

$\frac{(-1{)}^{m}mf(a)}{a^m{g}^{(m)}(a)}{\left(\frac{1}{a}\right)}^n{n}^{m-1}$

Proof

Proof due to Sedgewick and Wilf.

• $h(z)$, being meromorphic, can be Laurent expanded around $a$:

$h(z)=\frac{h_{-m}}{(z-a{)}^m}+\cdots +\frac{h_{-1}}{z-a}+h_0+h_1(z-a)+\cdots$

• this Laurent expansion can be estimated by its principle part:

$\frac{h_{-m}}{(z-a{)}^m}+\cdots +\frac{h_{-1}}{z-a}$

• $\frac{h_{-m}}{(z-a{)}^m}$ contributes the biggest coefficient. Its $n$th coefficient can be computed as:

$\frac{(-1{)}^m{h}_{-m}}{a^m}(\genfrac{}{}{0ex}{}{n+m-1}{n}){\left(\frac{1}{a}\right)}^n$

• $h_{-m}$ can be computed as:

$\underset{z\to a}{\lim }(z-a{)}^{m}h(z)=\frac{m!f(a)}{g^{(m)}(a)}$

• $(\genfrac{}{}{0ex}{}{n+m-1}{n})\sim \frac{n^{m-1}}{(m-1)!}$ as $n\to \mathrm{\infty }$ (Proof)
• Therefore, putting it all together:

$[z^n]h(z)\sim \frac{(-1{)}^m{h}_{-m}}{a^m}(\genfrac{}{}{0ex}{}{n+m-1}{n}){\left(\frac{1}{a}\right)}^n\sim \frac{(-1{)}^{m}mf(a)}{a^m{g}^{(m)}(a)}{\left(\frac{1}{a}\right)}^n{n}^{m-1}$ as $n\to \mathrm{\infty }$.

Asymptotic equality

We will make use of the asymptotic equality

$f(z)\sim g(z)$ as $z\to \zeta$

which means

$\underset{z\to \zeta }{\lim }\frac{f(z)}{g(z)}=1$

This allows us to use $g(z)$ as an estimate of $f(z)$ as $z$ gets closer to $\zeta$.

For example, we often present results of the form

$a_n\sim g(n)$ as $n\to \mathrm{\infty }$

which means, for large $n$, $g(n)$ becomes a good estimate of $a_n$.

Meromorphic function

The above theorem only applies to a class of generating functions called meromorphic functions. This includes all rational functions (the ratio of two polynomials) such as $\frac{1}{(1-z{)}^2}$ and $\frac{z}{1-z-z^2}$.

A meromorphic function is the ratio of two analytic functions. An analytic function is a function whose complex derivative exists.

One property of meromorphic functions is that they can be represented as Laurent series expansions, a fact we will use in the proof.

It is possible to estimate the coefficients of functions which are not meromorphic (e.g. $ln(z)$ or $e^z$). These will be covered in future chapters.

Laurent series

When we want a series expansion of a function $f(z)$ around a singularity $c$, we cannot use the Taylor series expansion. Instead, we use the Laurent series expansion:

$\cdots +\frac{a_{-2}}{(z-c{)}^2}+\frac{a_{-1}}{z-c}+a_0+a_1(z-c)+a_2(z-c{)}^2+\cdots$

Where $a_n=\frac{1}{2\pi i}\underset{\gamma }{\int }\frac{f(z)}{(z-c{)}^{n+1}}dz$ and $\gamma$ is a contour in the annular region in which $f(z)$ is analytic, illustrated below.

Pole

A pole is a type of singularity.

A singularity of $h(z)$ is a value of $z$ for which $h(z)=\mathrm{\infty }$

If $\underset{z\to a}{\lim }(z-a{)}^{m}h(z)=L\ne 0$ and $L$ is defined then $a$ is called a pole of $h(z)$ of order $m$.

We will make use of this fact when we calculate $h_{-m}$.

For example, $\frac{1}{(1-2z{)}^2}$ has the singularity $\frac{1}{2}$ because $\frac{1}{(1-2\frac{1}{2}{)}^2}=\frac{1}{(1-1{)}^2}=\frac{1}{0^2}=\frac{1}{0}=\mathrm{\infty }$ and $\frac{1}{2}$ is a pole of order 2 because $\underset{z\to \frac{1}{2}}{\lim }(z-\frac{1}{2}{)}^2\frac{1}{(1-2z{)}^2}=\underset{z\to \frac{1}{2}}{\lim }(z-\frac{1}{2}{)}^2\frac{1}{(-2{)}^2(z-\frac{1}{2}{)}^2}=\underset{z\to \frac{1}{2}}{\lim }\frac{1}{(-2{)}^2}=\frac{1}{4}$.

Closest to the origin

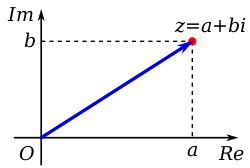
We are treating $h(z)$ as a complex function where the input $z$ is a complex number.

A complex number has two parts, a real part (Re) and an imaginary part (Im). Therefore, if we want to represent a complex number we do so in a two-dimensional graph.

If we want to compare the "size" of two complex numbers, we compare how far they are away from the origin in the two-dimensional plane (i.e. the length of the blue arrow in the above image). This is called the modulus, denoted $|z|$.

Principle part

Proof due to Wilf.

The principle part of a Laurent series expansion are the terms with a negative exponent, i.e.

$\frac{h_{-m}}{(z-a{)}^m}+\cdots +\frac{h_{-1}}{z-a}$

We will denote the principle part of $h(z)$ at $a$ by $PP(h,a)$.

If $a$ is the pole closest to the origin then the radius of convergence $R=|a|$ and as a consequence of the Cauchy-Hadamard theorem:

$[z^n]h(z)\le {(\frac{1}{|a|}+ϵ)}^n$ (for some $ϵ>0$ and for sufficiently large $n$)

$h(z)-PP(z)$ no longer has a pole at $a$ because $(\frac{h_{-m}}{(z-a{)}^m}+\cdots +\frac{h_{-}1}{z-a}+h_0+h_1(z-a)+\cdots )-(\frac{h_{-m}}{(z-a{)}^m}+\cdots +\frac{h_{-1}}{z-a})=h_0+h_1(z-a)+\cdots$.

If the second closest pole to the origin of $h(z)$ is $a^{\prime }$ then $a^{\prime }$ is the largest pole of $h(z)-PP(z)$ and, by the above theorem, the coefficients of $h(z)-PP(h,a)\le {(\frac{1}{|a^{\prime }|}+ϵ)}^n$ (for sufficiently large $n$).

Therefore, the coefficients of $PP(h,a)$ are at most different from the coefficient of $h(z)$ by ${(\frac{1}{|a^{\prime }|}+ϵ)}^n$ (for sufficiently large $n$).

Note that if $a$ is the only pole, the difference is at most ${ϵ}^n$ (for sufficiently large $n$).

If $|a^{\prime }|>|a|$ then as $n$ gets large ${\left(\frac{1}{|a^{\prime }|}\right)}^n$ will be much smaller than ${\left(\frac{1}{|a|}\right)}^n$ and, therefore, $PP(h,a)$ is a good enough approximation of $h(z)$.

However, if $|a^{\prime }|=|a|$ then the behaviour of the coefficients is more complicated.

Biggest coefficient

Compare:

$[z^n]\frac{h_{-m}}{(z-a{)}^m}=\frac{h_{-m}}{a^m}(\genfrac{}{}{0ex}{}{n+m-1}{n}){\left(\frac{1}{a}\right)}^n\sim \frac{h_{-m}}{a^m}{\left(\frac{1}{a}\right)}^n{n}^{m-1}$

with:

$[z^n]\frac{h_{-(m-1)}}{(z-a{)}^{m-1}}=\frac{h_{-(m-1)}}{a^{m-1}}(\genfrac{}{}{0ex}{}{n+m-2}{n}){\left(\frac{1}{a}\right)}^n\sim \frac{h_{-(m-1)}}{a^{m-1}}{\left(\frac{1}{a}\right)}^n{n}^{m-2}$

The $n$th coefficient of the former is only different to the latter by $O(\frac{n^{m-2}}{a^n})$.

Computation of coefficient of first term

$\frac{h_{-m}}{(z-a{)}^m}=\frac{(-1{)}^m{h}_{-m}}{a^m(1-\frac{z}{a}{)}^m}$ by factoring out ${\left(\frac{-1}{a}\right)}^m$.

$\frac{(-1{)}^m{h}_{-m}}{a^m(1-\frac{z}{a}{)}^m}=\frac{(-1{)}^m{h}_{-m}}{a^m}\sum _{n\ge 0}(\genfrac{}{}{0ex}{}{n+m-1}{n}){\left(\frac{z}{a}\right)}^n$ by the binomial theorem for negative exponents.

Computation of h_-m

$h(z)=\frac{h_{-m}}{(z-a{)}^m}+\frac{h_{-(m-1)}}{(z-a{)}^{m-1}}+\cdots +\frac{h_{-}1}{z-a}+h_0+h_1(z-a)+\cdots$.

Therefore, $\underset{z\to a}{\lim }(z-a{)}^{m}h(z)=\underset{z\to a}{\lim }{h}_{-m}+h_{-(m-1)}(z-a)+\cdots +h_{-}1(z-a{)}^{m-1}+h_0(z-a{)}^m+h_1(z-a{)}^{m+1}+\cdots =h_{-m}$.

To compute $\underset{z\to a}{\lim }(z-a{)}^{m}h(z)=\underset{z\to a}{\lim }\frac{(z-a{)}^{m}f(z)}{g(z)}$, because the numerator and denominator are both $0$ at $a$, we need to use L'Hôpital's rule:

$\underset{z\to a}{\lim }\frac{(z-a{)}^{m}f(z)}{g(z)}=\underset{z\to a}{\lim }\frac{((z-a{)}^{m}f(z){)}^{\prime }}{g^{\prime }(z)}$

Indeed, if $a$ is a root of order $m>1$ of $g(z)$ and $(z-a{)}^{m}f(z)$, it is also a root of $g^{\prime }(z)$ and $((z-a{)}^{m}f(z){)}^{\prime }$ and therefore $\underset{z\to a}{\lim }\frac{((z-a{)}^{m}f(z){)}^{\prime }}{g^{\prime }(z)}$ is also indeterminate. Therefore, we need to apply L'Hôpital's rule $m$ times:

$\underset{z\to a}{\lim }\frac{((z-a{)}^{m}f(z){)}^{(m)}}{g^{(m)}(z)}=\underset{z\to a}{\lim }\frac{((z-a{)}^m{f}^{\prime }(z)+m(z-a{)}^{m-1}f(z){)}^{(m-1)}}{g^{(m)}(z)}=\underset{z\to a}{\lim }\frac{((z-a{)}^m{f}^{″}(z)+2m(z-a{)}^{m-1}{f}^{\prime }(z)+m(m-1)(z-a{)}^{m-2}f(z){)}^{(m-2)}}{g^{(m)}(z)}=\cdots =\frac{m!f(a)}{g^{(m)}(a)}$

Proof of binomial asymptotics

$(\genfrac{}{}{0ex}{}{n+m-1}{n})=\frac{(n+m-1)!}{n!(m-1)!}=\frac{(n+1)(n+2)\cdots (n+m-1)}{(m-1)!}\sim \frac{n^{m-1}}{(m-1)!}$ as $n\to \mathrm{\infty }$.

References

• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite web
• Template:Cite web
• Template:Cite web
• Template:Cite book
• Template:Cite book
• Template:Cite book