Math for Non-Geeks/ Uniform continuity

{{#invoke:Math for Non-Geeks/Seite|oben}}

Uniform continuity is a stronger form of continuity. It is derived from the epsilon-delta criterion of continuity and particularly important for approximating functions.

Motivation

Recap: Epsilon-delta criterion

The definition of uniform continuity is built upon that one of the epsilon-delta criterion for continuity. We will therefore recap the epsilon-delta definition:

That is, if we choose an epsilon-tube around $f(x_0)$ , no matter how small it is, all function values in a sufficiently small environment of $x_0$ will lie in it. An epsilon-tube is an interval from $f(x_0)-ϵ$ to $f(x_0)+ϵ$ with $ϵ>0$ around$f(x_0)$:

A function f with an epsilon-tube around f(x_0)

A function $f:D\to ℝ$ is continuous at $x_0\in D$ if and only if for every epsilon-tube, there is a $\delta >0$ , such that all function values of $f$ when evaluated between $x_0-\delta$ and $x_0+\delta$ fit inside the epsilon-tube:

All function values for x between x_0-delta and x_0+delta fit inside the epsilon-tube around x_0

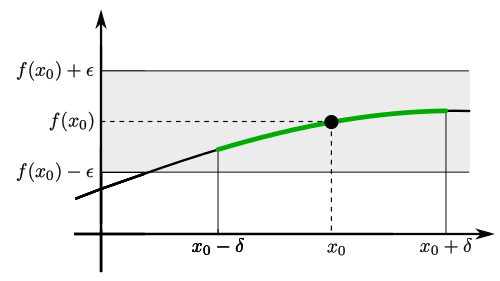
This $\delta$ may depend on the given function $f$, the given tube size $ϵ$and from the point $x_0$ . The following diagram shows an example, where a $\delta$-value is sufficiently small for $x_0$ , but too large for $x_1$ :

The value for delta is sufficiently small for x_0, but too large for x_1.

Hence, we must choose the $\delta$ at $x_1$ smaller. As both $\delta$-values at $x_0$ and $x_1$ are different, we will label them correspondingly by ${\delta }_0$ and ${\delta }_1$. This shows, that the $\delta$ within the definition of continuity may depend on the considered position $x$. The following diagram illustrates this:

Both the interval sizes delta_1 and delta_2 are sufficiently small for the given epsilon.

Derivation of uniform continuity

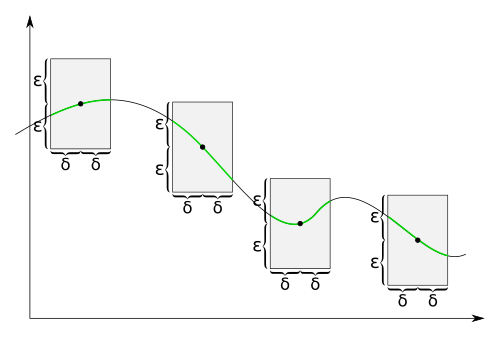
The epsilon-delta criterion guarantees that any continuous function $f:D\to ℝ$ can be approximated. For every maximal error $ϵ>0$ and around every $\tilde{x}$ we can find a ${\delta }_{\tilde{x}}>0$, such that the function value $f(x)$ at every $x$ inside the delta-interval $(\tilde{x}-\delta ,\tilde{x}+\delta )$ around $f(\tilde{x})$ maximally deviates from $f(\tilde{x})$ by $ϵ>0$. So for all of those $x$ with $\tilde{x}-\delta <x<\tilde{x}+\delta$ we can consider $f(\tilde{x})$ as an approximation of $f(x)$ with a maximal error of $ϵ$ . The following diagram illustrates this approximation at several points $x_i$:

Approximation of a continuous function at several positions.

However, the ${\delta }_{\tilde{x}}$-values depend on the considered position $\tilde{x}$ . This is why the rectangles in the above diagram have different sizes. For a more uniform approximation, we could impose additionally that all rectangles have to be of equal size, That means, the ${\delta }_{\tilde{x}}$-value shall be equally suitable for any $\tilde{x}$ . The above diagram would then look as follows:

Uniform approximation of a continuous function.

This is the core idea of uniform continuity. For any given $ϵ>0$ , there is a global $\delta >0$, such that no matter which point $\tilde{x}\in D$ is chosen, every function value $f(x)$ picked from the delta-interval $(\tilde{x}-\delta ,\tilde{x}+\delta )$ will be closer than $ϵ$ to $f(\tilde{x})$ . This leads us to the following definition of uniform continuity for a function $f:D\to ℝ$, which will allow us for uniform approximations:

Definition

Definition of uniform continuity

The formal definition of uniform continuity hence reads as follows:

In different words, for each $ϵ>0$ there is a $\delta >0$ , such that all pairs $x,\tilde{x}\in D$ with $|x-\tilde{x}|<\delta$ satisfy the inequality $|f(x)-f(\tilde{x})|<ϵ$ .

Quantifier notation

The commented version of the quantifier notation reads:

Comparing the epsilon-delta definition of uniform continuity and continuity in the quantifier notation, we notide that only two quantifiers have been permuted:

The reason is that the $\delta$ used for uniform continuity is a global one, i.e. it does not depend on the position $\tilde{x}\in D$ . In order to express this independence, the existence quantifier „$\mathrm{\exists }\delta >0$“ must appear in front of the all quantifier „$\mathrm{\forall }\tilde{x}\in D$“ .

Deriving the negation of uniform continuity

The quantifier notation is a handy tool for inverting definitions - like for uniform continuity. It basically works by step-wise replacing existence and all quantifiers by the respective other expression:

So:

Uniform continuity is a global property

Uniform continuity is a global property of a function. That means, it makes only sense to consider uniform continuity of a whole function. By contrast, continuity is a local property. We can speak of a function being continuous at a certain position $x$. For uniform continuity, this is not possible. However, a function can be both be globally continuous (continuous at every $x\in D$) and (globally) uniformly continuous.

The globalness is just a consequence from the definition: For uniform continuity, we can find a global $\delta >0$, whose delta-interval around every argument is a sufficient approximation. It is no necessary to speak of a global delta at some certain argument $x$: we just need to find one delta for all arguments.

Visualization

Recap: visaulization of the epsilon-delta criterion

In order to visualize the epsilon-delta criterion, we will draw a rectangle centred at $(x_0,f(x_0))$ with height $2ϵ$ and width $2\delta$. In order to satisfy the epsilon-delta criterion, the graph must not lie above or below the rectangle, but completely inside:

The 2epsilon-2delta rectangle with permitted and non-permitted area

Take, for instance the square function at arguments around $x_0=1$. No matter how small we impose $ϵ$ , we can always find a $\delta$, such that the graph lies completely in the interior of the $2ϵ$-$2\delta$-rectangle:

Visualization of the epsilon-delta criterion for the square function

Conversely, if a function is not continuous, such as the sign function $\mathrm{sgn}(x)$ , we are able to find an $ϵ>0$, whose graph always takes values above or below the rectangle - no matter how narrow we make it. Concerning the sign function at $x_0=0$ , this will for instance be the case if we choose $ϵ=\frac{1}{2}$ :

• 
  For $ϵ=\frac{1}{2}$ and $\delta =1$ , the sign function has function values above and below the $2ϵ$-$2\delta$-rectangle (marked in red).
• 
  No matter how small we choose $\delta$ , there are always points on the graph above or below the $2ϵ$-$2\delta$-rectangle.

Visualization of uniform continuity

For uniformly continuous functions, we can draw one rectangle with heighth $2ϵ$ and width $2\delta$ and move it to any point on the graph, without having pieces of the graph above or below the rectangle. The function $f(x)=\sqrt{x}$ is uniformly continuous. Despite having infinite derivative at zero, the graph always runs inside the upper and lower bounds of the rectangle. However, for $g(x)=\frac{1}{x}$ this is not the case. In the vicinity of arguments near zero, the function moves infinitely far into the $y$-direction. No matter how narrow we choose the rectangle, the function will always break its lower and upper barriers for $x$ close enough to zero.

For uniform continuity, $\delta$ has to be the same at every $x$ . The graph has to fit inside the rectangle, no matter where we move it. That means: For every $ϵ>0$ there must be a $\delta >0$ , such that the $2ϵ$-$2\delta$-rectangle can be moved arbitrarily along the graph without having function values above or below it:

For a uniformly continuous function, there is no point above or below the rectangle - no matter where on the graph we place it.

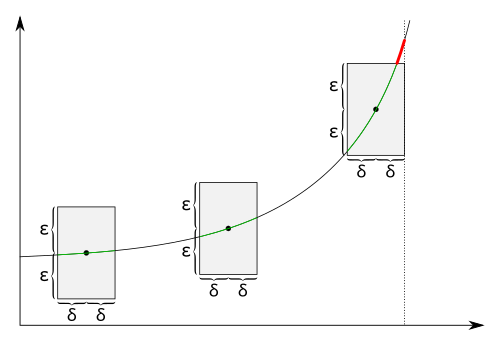
For a non-uniformly continuous function, this is not possible. Anoter counter-example is the square function. In fact, for any given $ϵ>0$ (not just a specific one), we cannot find a $\delta >0$ , such that the graph does nowhere cross the upper or lower border of the $2ϵ$-$2\delta$-rectangle. For $x$-values near zero, the square function is close to constant, so the graph will fit inside some $2ϵ$-$2\delta$-rectangle, there. But the more we move it to the right, the steeper our function will get. And at some point, the function will break the upper and lower barriers of the $2ϵ$-$2\delta$-rectangle. So the square function in a continuous but not uniformly continuous function:

The square function is a continuous but not uniformly continuous function.

Scheme of proof

Scheme of proof: Uniform continuity

In terms of quantifiers, the definition of uniform continuity reads:

This can be used to derive a scheme of proof for uniform continuity:

Scheme of proof: Not uniformly continuous

In terms of quantifiers, the definition of $f$ being not uniformly continuous reads:

This can be used to derive a scheme for disproving uniform continuity:

Uniform continuity as a stronger form of continuity

Uniform continuity is a stronger form of continuity. That means, every uniformly continuous function is also continuous. The converse does not hold. There are functions like the square function $f:ℝ\to ℝ:x\mapsto x^2$ being continuous, but not uniformly continuous:

The square function is continuous but not uniformly continuous

As we have seen, every uniformly continuous function is also continuous. However, the converse does not hold. Let us consider again the square function as an example:Template:Math

As we have seen in the section visualization, if there is $ϵ>0$ given, we cannot set a fixed $\delta >0$ , such that the graph is everywhere inside the $2ϵ$-$2\delta$-rectangle , independent from where we place it. The further we move the rectangle to the right, the steeper the square function gets. And at some point, the graph starts crossing he upper and lower borders of the $2ϵ$-$2\delta$-rectangle.

This can also be seen by checking the epsilon-delta definition of uniform continuity: $\mathrm{\forall }ϵ>0\mathrm{\exists }\delta >0\mathrm{\forall }\tilde{x}\in ℝ\mathrm{\forall }x\in ℝ:|x-\tilde{x}|<\delta ⟹|f(x)-f(\tilde{x})|<ϵ$. We want to prove the negation of this statement, i.e. $\mathrm{\exists }ϵ>0\mathrm{\forall }\delta >0\mathrm{\exists }\tilde{x}\in ℝ\mathrm{\exists }x\in ℝ:|x-\tilde{x}|<\delta$ and $|f(x)-f(\tilde{x})|\ge ϵ$. Consider for instance $ϵ=1$ and assume there was some $\delta >0$, such that $|x_1^2-x_0^2|<ϵ$ for all real numbers $x_0,x_1\in ℝ$ with $|x_1-x_0|<\delta$ . Now consider some $x_0(\delta )>0$ which we will determine later. We take the centre $x_0$ and some point $x_1:=x_0+\frac{\delta }{2}$ inside the $\delta$-interval. That means, $|x_1-x_0|=\frac{\delta }{2}<\delta$.

Now, we want to show that $|x_1^2-x_0^2|\ge ϵ$ holds.

Further,

If we choose $x_0\ge \frac{1}{\delta }$ then it is guaranteed that $|x_1^2-x_0^2|\ge 1=ϵ$. Hence, we have proven that

is not uniformly continuous.

Example: uniformly continuous functions

• The identity function $f:D\to D$ is uniformly continuous, since for $|x-y|<\delta$ , we can show $|f(x)-f(y)|=|x-y|<ϵ$ by choosing $\delta =ϵ$ .

• Above, we have seen that the square function $f:ℝ\to ℝ$ is not uniformly continuous on the real numbers. However, when restricting to a compact interval, the function gets uniformly continuous. For example,

Template:Math is uniformly continuous. We can prove this as follows: There is Template:Math because $x,y\in [0,1]$ . So we can choose $\delta :=\frac{ϵ}{2}$ and then for all $x,y\in D$ with $|x-y|<\delta$ the estimate $|f(x)-f(y)|<2|x-y|<2\delta =ϵ$ will hold.

• The square root function is uniformly continuous on ${ℝ}_0^{+}$. Consider:

Template:Math Let $ϵ>0$ be arbitrary. Then, $\delta ={ϵ}^2$ is a suitable choice: Let $x,y\in [0,\mathrm{\infty }[$ with $|x-y|<\delta$.

Without any restrictions, we may choose $x\le y$. Then, there is also $\sqrt{x}\le \sqrt{y}$, and hence we get $|\sqrt{x}-\sqrt{y}|=\sqrt{y}-\sqrt{x}$.

Now, we want to prove that $|f(x)-f(y)|=|\sqrt{x}-\sqrt{y}|=\sqrt{y}-\sqrt{x}<ϵ$ .

By assumption there is $0\le x\le y<x+{ϵ}^2$. And therefore:

So $y<(\sqrt{x}+ϵ{)}^2$. Since by assumption $x,y\ge 0$ and also $ϵ>0$ , we may take the square root of this equation and obtain $\sqrt{y}<\sqrt{x}+ϵ$, i.e.$\sqrt{y}-\sqrt{x}<ϵ$, which is what we wanted to show. Hence, we have proven that $f$ is uniformly continuous.

• The following example is not uniformly continuous:

Template:Math , which are sine waves oscillating faster and faster when approaching $x=0$. Assume that $f$ was uniformly continuous. Then we could find some global $\delta$ such that the epsilon-delta criterion holds everywhere. But now, for $x\to 0$ the frequency of $f$ gets arbitrarily high, so inside an interval close to $x\to 0$ , there will always be a full oscillation of the sine inside any $\delta$-ball. Since the peak-to-peak amplitude of the sine function is equal to $2$ , the condition $|f(x)-f(y)|<ϵ$ will never hold everywhere for $ϵ<2$ . We just have to move the rectangle close enough to 0, as illustrated by the subsequent figure:

This image shows, that the topological sine curve is not uniformly continuous. For an environment of fixed width and x going towards 0, at some point a full period will be inside the environment.

Properties

As we have seen, not every continuous function is also uniformly continuous. But if we restrict to a closed, compact interval $[a,b]$ , both continuity and uniform continuity will be equivalent:

{{#invoke:Math for Non-Geeks/Seite|unten}}