Formal Logic/Sentential Logic/Properties of Sentential Connectives
Template:Formal Logic:TOCPageNav
Properties of Sentential Connectives
Here we list some of the more famous, historically important, or otherwise useful equivalences and tautologies. They can be added to the ones listed in Interdefinability of connectives. We can go on at quite some length here, but will try to keep the list somewhat restrained. Remember that for every equivalence of and , there is a related tautology .
Bivalence
Every formula has exactly one of two truth values.
- Law of Excluded Middle
- Law of Non-Contradiction
Analogues to arithmetic laws
Some familiar laws from arithmetic have analogues in sentential logic.
Reflexivity
Conditional and biconditional (but not conjunction and disjunction) are reflexive.
Commutativity
Conjunction, disjunction, and biconditional (but not conditional) are commutative.
Associativity
Conjunction, disjunction, and biconditional (but not conditional) are associative.
Distribution
We list ten distribution laws. Of these, probably the most important are that conjunction and disjunction distribute over each other and that conditional distributes over itself.
Transitivity
Conjunction, conditional, and biconditional (but not disjunction) are transitive.
Other tautologies and equivalences
Conditionals
These tautologies and equivalences are mostly about conditionals.
Biconditionals
These tautologies and equivalences are mostly about biconditionals.
Miscellaneous
We repeat DeMorgan's Laws from the Interdefinability of connectives section of Expressibility and add two additional forms. We also list some additional tautologies and equivalences.
- Idempotence for conjunction
- Idempotence for disjunction
- Disjunctive addition
- Disjunctive addition
-
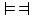 Demorgan's Laws
Demorgan's Laws -
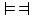 Demorgan's Laws
Demorgan's Laws -
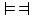 Demorgan's Laws
Demorgan's Laws -
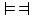 Demorgan's Laws
Demorgan's Laws -
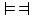 Double Negation
Double Negation
Deduction and reduction principles
The following two principles will be used in constructing our derivation system on a later page. They can easily be proven, but—since they are neither tautologies nor equivalences—it takes more than a mere truth table to do so. We will not attempt the proof here.
Deduction principle
Let and both be formulae, and let be a set of formulae.
Reduction principle
Let and both be formulae, and let be a set of formulae.