A-level Mathematics/OCR/C2/Trigonometric Functions

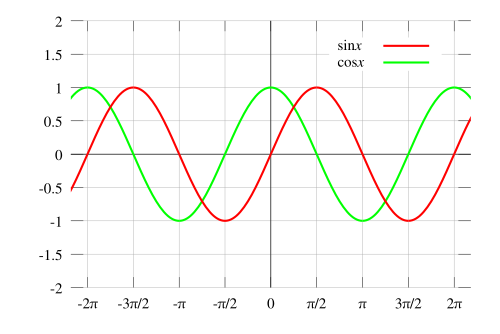
The Trigonometric Ratios Of An Angle

We use the triangle on the left to define the three basic trigonometric ratios, using angle A. A good mnemonic is the acronym SOHCAHTOA, Sin Opposite Hypotenuse, Cosine Adjacent Hypotenuse, Tangent Opposite Adjacent. Remember if you are using a calculator to obtain the value of a trigonometric ratio make sure that it is in the proper mode; it should be in radian mode if the angle is in radians and degree mode if the angle is in degrees. You can find the angle that corresponds to a value using the inverse of each function usually listed as ${\cos }^{-1},{\sin }^{-1},{\tan }^{-1}$ on your calculator, a formal discussion of the inverse trigonometric functions will be in Core 3. The vertical blue dashed lines in the tangent graph are the asymptotes of the tangent function. The tangent function will not be defined at these points because at these points the cosine graph is zero, see the tangent identity.

Function	Written	Defined	Graph
Cosine	$\cos \theta$	$\frac{Adjacent}{Hypotenuse}$
Sine	$\sin \theta$	$\frac{Opposite}{Hypotenuse}$
Tangent	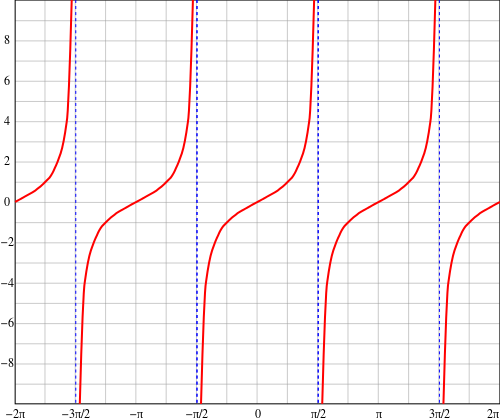$\tan \theta$	$\frac{Opposite}{Adjacent}$

The CAST Model

The Cast Model is used to show in which quadrant a trigonometric ratio will be positive. A mnemonic is All Students Take Core 4. The four indicates that Cosine is in the fourth quadrant. Also you need to know that sin(x) = sin(π rad or 180° - x) = c, cos(x) = cos(2π rad or 360° - x) = c, and tan(x) = tan(π rad or 180° + x)= c. This is important to remember because if sin(x) = 1/2, and it is between 0° and 360° then x can be 30° or 150°.

Important Trigonometric Values

Below is a table with the common trigonometric values (The circle is labelled with the same values), you need to have these values memorized. $\theta$ $rad$ $\sin \theta$ $\cos \theta$ $\tan \theta$ $0^{\circ }$ 0 0 1 0 $30^{\circ }$ $\frac{\pi }{6}$ $\frac{1}{2}$ $\frac{\sqrt{3}}{2}$ $\frac{1}{\sqrt{3}}$ $45^{\circ }$ $\frac{\pi }{4}$ $\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$ $1$ $60^{\circ }$ $\frac{\pi }{3}$ $\frac{\sqrt{3}}{2}$ $\frac{1}{2}$ $\sqrt{3}$ $90^{\circ }$ $\frac{\pi }{2}$ 1 0 None

The Law of Cosines

Pythagoras theory only applies to right triangles, the law of cosines will apply to any triangle. When you have a right triangle it reduces to the same formula as given by Pythagoras theorem. For any triangle ABC with angle measurement

$\alpha$

,

$\beta$

,

$\gamma$

and sides of length a,b,c.

Template:TrigBoxOpen $a^2=b^2+c^2-2bc\cos \alpha$
$b^2=a^2+c^2-2ac\cos \beta$
$c^2=a^2+b^2-2ab\cos \gamma$ Template:TrigBoxClose

Example

What is the value of c when a = 4 cm, b = 8 cm, and $\gamma$ is equal to $64^{\circ }$. $c^2=4^2+8^2-2\times 4\times 8\cos 64^{\circ }$

$c^2=53$

$c\approx 7.28cm$

The Law of Sines

For any triangle ABC with angle measurement $\alpha$, $\beta$, $\gamma$ and sides of length a,b,c.

Template:TrigBoxOpen $\frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }$ Template:TrigBoxClose

Example If Angle α is $45^{\circ }$, Angle β is $24^{\circ }$ and Side b is 3 cm, what is the length of side a?

$\frac{a}{\sin 45^{\circ }}=\frac{3}{\sin 24^{\circ }}$

$a\times \sin 24^{\circ }=3\times \sin 45^{\circ }$

$a=\frac{3\times \sin 45^{\circ }}{\sin 24^{\circ }}\approx 5.22\text{cm}$

Area of a Triangle

For any triangle the area is one-half the product of two sides with the sine of the included angle. If the included angle is a right angle, then this reduces to the formula for the area of a right triangle, since $\sin 90^{\circ }=1$

Template:TrigBoxOpen $Area=\frac{1}{2}bc\sin \alpha$

$Area=\frac{1}{2}ac\sin \beta$

$Area=\frac{1}{2}ab\sin \gamma$ Template:TrigBoxClose

Example:

What is the area of triangle when a = 4 cm, b = 8 cm, and $\gamma$ is equal to $20^{\circ }$.

$Area=\frac{1}{2}\times 4\times 8\times \sin 20^{\circ }\approx 5.47{\text{cm}}^2$

Pythagoras Identity

Template:TrigBoxOpen ${\sin }^2\theta +{\cos }^2\theta =1$ Template:TrigBoxClose

Proof:

We use the pythagorean theory:

$a^2+b^2=c^2$

Now we divide by $c^2$:

$\frac{a^2}{c^2}+\frac{b^2}{c^2}=\frac{c^2}{c^2}$

We get:

$\frac{a^2}{c^2}+\frac{b^2}{c^2}=1$

We can write this as:

${\sin }^2\theta +{\cos }^2\theta =1$

A good way to think of this of is $opposit{e}^2+adjacen{t}^2=hypotenus{e}^2=\frac{opposit{e}^2}{hypotenus{e}^2}+\frac{adjacen{t}^2}{hypotenus{e}^2}=1$

A Practical Example

Find all the values of x between 0 rad and 2π rad that satisfy the relationship $15{\sin }^2\left(x\right)=\cos \left(x\right)+13$.

Using the Pythagoras Identity we get:

$15(1-{\cos }^2\left(x\right))=\cos \left(x\right)+13$

Now we can simplify:

$15{\cos }^2\left(x\right)-\cos \left(x\right)-2=0$

It is more covinent to replace cos(x) with u:

$15u^2-u-2=0$

Then we factor the expression

$(5u+2)(3u-1)=0$

$\cos \left(x\right)=\frac{-2}{5}or\frac{1}{3}$

In order to determine what x is we need to use ${\cos }^{-1}\left(x\right)$ on our calculators.

${\cos }^{-1}\left(\frac{-2}{5}\right)\approx 1.9823rad$

${\cos }^{-1}\left(\frac{1}{3}\right)\approx 1.2310rad$

But we need to remember that in the interval 2π the cosine function will have the same in 2π - x.

2π rad - 1.2310 rad = 5.0222 rad

2π rad - 1.9823 rad = 4.3009 rad

So the complete answer is 1.2310 rad, 1.9823 rad, 4.3009 rad, and 5.0222 rad.

Tangent Identity

Template:TrigBoxOpen $\tan \theta =\frac{\sin \theta }{\cos \theta }$ Template:TrigBoxClose

Proof:

$\tan \theta =\frac{a}{b}$

Then we can divide both the numerator and the denominator by c

$\tan \theta =\frac{\frac{a}{c}}{\frac{b}{c}}$

We can write this as:

$\tan \theta =\frac{\sin \theta }{\cos \theta }$

Example

sin(x) = 4cos(x) solve for sin(x). All units are in radians.

We divide both sides by cos x and we get the identity

tan(x)=4

We use the $ta{n}^{-1}(x)$ to get that x = 1.3258 rad.

Now we can solve for sin(x):

sin(x) = 4cos(1.3258 rad) = 4*.2425 rad = .9701 rad .