File:Gaussianprocess SensorCalibrationCurvesMean.svg
From testwiki
Jump to navigation
Jump to search

Size of this PNG preview of this SVG file: 306 × 230 pixels. Other resolutions: 319 × 240 pixels | 639 × 480 pixels | 1,022 × 768 pixels | 1,280 × 962 pixels | 2,560 × 1,924 pixels.
Original file (SVG file, nominally 306 × 230 pixels, file size: 27 KB)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionGaussianprocess SensorCalibrationCurvesMean.svg |
Deutsch: Mean and standard deviation of sample set |
| Date | |
| Source | Own work |
| Author | Physikinger |
| SVG development InfoField | |
| Source code InfoField | Python code#This source code is public domain
#Author: Christian Schirm
import numpy, scipy.spatial
import matplotlib.pyplot as plt
numpy.random.seed(1)
def covMat(x1, x2, covFunc, noise=0): # Covariance matrix
cov = covFunc(scipy.spatial.distance_matrix(numpy.atleast_2d(x1).T, numpy.atleast_2d(x2).T))
if noise: cov += numpy.diag(numpy.ones(len(cov))*noise)
return cov
N=15
x = numpy.linspace(0, 10, 100)
y = [4*x**.7*(0.3+0.4*numpy.random.rand()) + (numpy.random.rand()-0.5)*2.8*numpy.sin(0.3*x*(1+0.05*numpy.random.rand())) for i in range(N)]
fig = plt.figure(figsize=(4.*0.85,3*0.85),dpi=100)
for i,iy in enumerate(y): plt.plot(x,iy,color=plt.cm.tab10(i*1./N))
plt.xlabel(u'Physical Value x')
plt.ylabel('Sensor Signal')
plt.axis([0,10,0,12])
plt.tight_layout()
plt.savefig('Gaussianprocess_SensorCalibrationCurves.svg')
A = numpy.array(y)
m = numpy.mean(A,axis=0)
cov = (A-m).T.dot((A-m))/(len(A)-1)
sigma = numpy.sqrt(cov.diagonal())
fig = plt.figure(figsize=(4.*0.85,3*0.85),dpi=100)
plt.fill_between(x, m - sigma, m + sigma, color = '0.85')
plt.plot(x,m,'-')
plt.xlabel(u'Physical Value x')
plt.ylabel('Sensor Signal')
plt.axis([0,10,0,12])
plt.tight_layout()
plt.savefig('Gaussianprocess_SensorCalibrationCurvesMean.svg')
iTest = numpy.array([45, 95])
yTest = m[iTest] + [+0.5,+2]
mask = numpy.zeros(len(cov),'bool')
mask[iTest[-1:]] = True
Ckk = cov[mask][:,mask]
Cuu = cov
numpy.fill_diagonal(Cuu,numpy.diag(Cuu)+0.000001)
CkkInv = numpy.linalg.inv(Ckk)
Cuk = cov[:,mask]
yPred = m + numpy.dot(numpy.dot(Cuk,CkkInv), yTest[-1:] - m[mask])
sigma = numpy.sqrt(numpy.maximum(0,numpy.diag(Cuu - numpy.dot(numpy.dot(Cuk,CkkInv),Cuk.T))))
fig = plt.figure(figsize=(4.*0.85,3*0.85),dpi=100)
plt.fill_between(x, yPred - sigma, yPred + sigma, color = '0.85')
plt.plot(x,yPred,'-')
plt.plot(x[mask],yTest[-1:],'ko')
plt.xlabel(u'Physical Value x')
plt.ylabel('Sensor Signal')
plt.axis([0,10,0,12])
plt.tight_layout()
plt.savefig('Gaussianprocess_SensorCalibration1Point.svg')
mask = numpy.zeros(len(cov),'bool')
mask[iTest] = True
Ckk = cov[mask][:,mask]
Cuu = cov
numpy.fill_diagonal(Cuu,numpy.diag(Cuu)+0.000001)
CkkInv = numpy.linalg.inv(Ckk)
Cuk = cov[:][:,mask]
yPred = m + numpy.dot(numpy.dot(Cuk,CkkInv), yTest - m[mask])
sigma = numpy.sqrt(numpy.maximum(0,numpy.diag(Cuu - numpy.dot(numpy.dot(Cuk,CkkInv),Cuk.T))))
fig = plt.figure(figsize=(4.*0.85,3*0.85),dpi=100)
plt.fill_between(x, yPred - sigma, yPred + sigma, color = '0.85')
plt.plot(x,yPred,'-')
plt.plot(x[mask],yTest,'ko')
plt.xlabel(u'Physical Value x')
plt.ylabel('Sensor Signal')
plt.axis([0,10,0,12])
plt.tight_layout()
plt.savefig('Gaussianprocess_SensorCalibration2Point.svg')
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
some value
1 March 2018
image/svg+xml
28,004 byte
bcf7da8e5b0519ea5e156c4b31962aa8d891fcd3
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 22:26, 23 March 2023 | 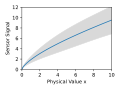 | 306 × 230 (27 KB) | wikimediacommons>Physikinger | English |
File usage
The following page uses this file: