File:Mandelbrot numpy set 3.png
From testwiki
Jump to navigation
Jump to search

Size of this preview: 800 × 600 pixels. Other resolutions: 320 × 240 pixels | 640 × 480 pixels | 1,024 × 768 pixels | 1,280 × 960 pixels | 2,560 × 1,920 pixels.
Original file (2,560 × 1,920 pixels, file size: 3.03 MB, MIME type: image/png)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionMandelbrot numpy set 3.png |
Deutsch: Die Mandelbrot-Menge wird mit NumPy unter Verwendung komplexer Matrizen berechnet. Es wird eine von David Madore und Anders Sandberg vorgestellte logarithmische Projektion verwendet. Die so erstellten Bilder werden auch Exponential Maps oder Mercator-Mandelbrot Maps genannt. Durch diese Projektion lässt sich die Berechnung von Zoom-Animationen sehr vereinfachen. English: The Mandelbrot set is calculated with NumPy using complex matrices. A logarithmic projection presented by David Madore and Anders Sandberg is used. The images created in this way are also called Exponential Maps or Mercator-Mandelbrot Maps. This projection makes the calculation of zoom animations much easier |
| Date | |
| Source | Own work |
| Author | Majow |
| Other versions |
|
| PNG development InfoField | |
| Source code InfoField | Python codeimport numpy as np
import matplotlib.pyplot as plt
d, h = 200, 1000 # pixel density (= image width) and image height
n, r = 800, 5000 # number of iterations and escape radius (r > 2)
a = -1.748764520194788535 # coordinates by Claude Heiland-Allen
b = 3e-13 # https://mathr.co.uk/web/m-location-analysis.html
x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)
A, B = np.meshgrid(x * np.pi, y * np.pi)
C = 4.0 * np.exp((A + B * 1j) * 1j) + (a + b * 1j)
def iteration(C):
Z, dZ = np.zeros_like(C), np.zeros_like(C)
def iterate5(C, Z, dZ):
Z, dZ = Z * Z + C, 2 * Z * dZ + 1
Z, dZ = Z * Z + C, 2 * Z * dZ + 1
Z, dZ = Z * Z + C, 2 * Z * dZ + 1
Z, dZ = Z * Z + C, 2 * Z * dZ + 1
Z, dZ = Z * Z + C, 2 * Z * dZ + 1
return Z, dZ
for i in range(0, n, 5):
M = abs(Z) < r
Z[M], dZ[M] = iterate5(C[M], Z[M], dZ[M])
return Z, dZ
Z, dZ = iteration(C)
D = np.zeros(C.shape)
fig = plt.figure(figsize=(12.8, 9.6))
fig.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.95)
N = abs(Z) > 2 # exterior distance estimation
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])
ax1 = fig.add_subplot(3, 1, 1)
ax1.imshow(D.T ** 0.05, cmap=plt.cm.nipy_spectral, origin="lower")
M = 50 * (2 / d) * np.pi * np.exp(- B) # adjust marker size 50 as needed
k, l = min(d, h) + 1, max(0, h - d) // 8 # adjust zoom level 8 as needed
for i in range(8):
X, Y = C[i*l:i*l+k, 0:d].real, C[i*l:i*l+k, 0:d].imag
S, T = M[0:k, 0:d] ** 2, D[i*l:i*l+k, 0:d] ** 0.5
ax = fig.add_subplot(3, 4, 5 + i)
ax.scatter(X, Y, s=S, c=T, cmap=plt.cm.nipy_spectral)
ax.set_xticks([])
ax.set_yticks([])
ax.axis('equal')
fig.savefig("Mandelbrot_numpy_set_3.png", dpi=200)
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Computing the Mandelbrot set with NumPy and complex matrices (Part 3)
Berechnung der Mandelbrot-Menge mit NumPy und komplexen Matrizen (Teil 3)
Items portrayed in this file
depicts
24 September 2023
image/png
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 23:35, 24 September 2023 | 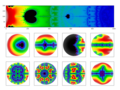 | 2,560 × 1,920 (3.03 MB) | wikimediacommons>Majow | Uploaded own work with UploadWizard |
File usage
The following page uses this file:

