File:Mandelbrot numpy set 4.png
From testwiki
Jump to navigation
Jump to search

Size of this preview: 800 × 100 pixels. Other resolutions: 320 × 40 pixels | 2,560 × 320 pixels.
Original file (2,560 × 320 pixels, file size: 201 KB, MIME type: image/png)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionMandelbrot numpy set 4.png |
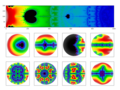
Deutsch: Die Mandelbrot-Menge wird mit NumPy unter Verwendung komplexer Matrizen berechnet. Für die extreme Zoomtiefe der Mercator-Map wird eine von Kevin Martin (2013) und Zhuoran Yu (2021) vorgestellte Berechnungsmethode verwendet: Störungsrechnung mit dynamischer Umbasierung. English: The Mandelbrot set is calculated with NumPy using complex matrices. For the extreme zoom depth of the Mercator map, a calculation method presented by Kevin Martin (2013) and Zhuoran Yu (2021) is used: perturbation theory with dynamic rebasing. |
| Date | |
| Source | Own work |
| Author | Majow |
| Other versions |
|
| PNG development InfoField | |
| Source code InfoField | Python codeimport numpy as np
import matplotlib.pyplot as plt
import decimal as dc # decimal floating point arithmetic with arbitrary precision
dc.getcontext().prec = 80 # set precision to 80 digits (about 256 bits)
d, h = 50, 1000 # pixel density (= image width) and image height
n, r = 80000, 100000 # number of iterations and escape radius (r > 2)
a = dc.Decimal("-1.256827152259138864846434197797294538253477389787308085590211144291")
b = dc.Decimal(".37933802890364143684096784819544060002129071484943239316486643285025")
S = np.zeros(n + 5, dtype=np.complex128) # 5 iterations are chained
u, v = dc.Decimal(0), dc.Decimal(0)
for i in range(n + 5):
S[i] = float(u) + float(v) * 1j
if u * u + v * v < r * r:
u, v = u * u - v * v + a, 2 * u * v + b
else:
print("The reference sequence diverges within %s iterations." % i)
break
x = np.linspace(0, 2, num=d+1, dtype=np.float64)
y = np.linspace(0, 2 * h / d, num=h+1, dtype=np.float64)
A, B = np.meshgrid(x * np.pi, y * np.pi)
C = (- 8.0) * np.exp((A + B * 1j) * 1j)
def iteration(S, C):
I = np.zeros(C.shape, dtype=np.intp)
E, Z, dZ = np.zeros_like(C), np.zeros_like(C), np.zeros_like(C)
def iterate5(C, I, E, Z, dZ):
I, E = I + 1, (2 * S[I] + E) * E + C
Z, dZ = S[I] + E, 2 * Z * dZ + 1
I, E = I + 1, (2 * S[I] + E) * E + C
Z, dZ = S[I] + E, 2 * Z * dZ + 1
I, E = I + 1, (2 * S[I] + E) * E + C
Z, dZ = S[I] + E, 2 * Z * dZ + 1
I, E = I + 1, (2 * S[I] + E) * E + C
Z, dZ = S[I] + E, 2 * Z * dZ + 1
I, E = I + 1, (2 * S[I] + E) * E + C
Z, dZ = S[I] + E, 2 * Z * dZ + 1
return I, E, Z, dZ
for i in range(0, n, 5):
aZ, aE = abs(Z), abs(E)
M, R = aZ < r, aZ < aE
I[R], E[R] = 0, Z[R] # reset the reference orbit
I[M], E[M], Z[M], dZ[M] = iterate5(C[M], I[M], E[M], Z[M], dZ[M])
return I, E, Z, dZ
I, E, Z, dZ = iteration(S, C)
D = np.zeros(C.shape, dtype=np.float64)
fig = plt.figure(figsize=(12.8, 1.6))
fig.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.95)
N = abs(Z) > 2 # exterior distance estimation
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])
ax1 = fig.add_subplot(1, 1, 1)
ax1.imshow(D.T ** 0.015, cmap=plt.cm.nipy_spectral, origin="lower")
fig.savefig("Mandelbrot_numpy_set_4.png", dpi=200)
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Computing the Mandelbrot set with NumPy and complex matrices (Part 4)
Berechnung der Mandelbrot-Menge mit NumPy und komplexen Matrizen (Teil 4)
Items portrayed in this file
depicts
24 September 2023
image/png
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 23:35, 24 September 2023 | 2,560 × 320 (201 KB) | wikimediacommons>Majow | Uploaded own work with UploadWizard |
File usage
The following page uses this file: