A-level Mathematics/AQA/MFP3

Series and limits

Two important limits:

$\underset{x\to \mathrm{\infty }}{\lim }\left(x^k{e}^{-x}\right)\to 0$ for any real number k

$\underset{x\to 0}{\lim }(x^k\ln x)\to 0$ for all k > 0

The basic series expansions

$(r=0,1,2,\cdots )$

$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots +\frac{x^r}{r!}+\cdots$

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots +{(-1)}^r\frac{x^{2r+1}}{(2r+1)!}+\cdots$

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots +{(-1)}^{r+1}\frac{x^{2r}}{(2r)!}+\cdots$

$(1+x{)}^n=1+nx+\frac{n(n-1)}{2!}{x}^2+\cdots +(\genfrac{}{}{0ex}{}{n}{r})x^r+\cdots$

$(r=1,2,3,\cdots )$

$\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots +(-1{)}^{r+1}\frac{x^r}{r}+\cdots$

Improper intergrals

The integral :$\underset{a}{\overset{b}{\int }}f(x)dx$ is said to be improper if

1. the interval of integration is infinite, or;
2. f(x) is not defined at one or both of the end points x=a and x=b, or;
3. f(x) is not defined at one or more interior points of the interval $a\le x\le b$.

Polar coordinates

A diagram illustrating the relationship between polar and Cartesian coordinates.

$x=r\cos \theta ,$

$y=r\sin \theta ,$

$r^2=x^2+y^2,$

$\tan \theta =\frac{y}{x}$

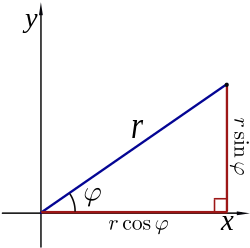
The area bounded by a polar curve

For the curve $r=f(\theta ),$ $\alpha \le \theta \le \beta .$

$A=\underset{\alpha }{\overset{\beta }{\int }}\frac{1}{2}{r}^{2}d\theta$

r must be defined and be non-negative throughout the interval $\alpha \le \theta \le \beta .$

Numerical methods for the solution of first order differential equations

Euler's formula

$y_{r+1}=y_r+hf(x_r,y_r)$

The mid-point formula

$y_{r+1}=y_{r-1}+2hf(x_r,y_r)$

The improved Euler formula

$y_{r+1}=y_r+\frac{1}{2}(k_1+k_2)$

where

$k_1=hf(x_r,y_r)$

and

$k_2=hf(x_r+h,y_r+k_1).$

Further reading

The AQA's free textbook [1]