Electronics Handbook/Circuits/RLC Series

RLC Series

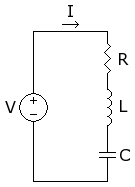
Circuit Analysis

Circuit's Impedance

$Z=Z_R+Z_L+Z_C$

$Z=R+j\omega L+\frac{1}{j\omega C}$

$Z=\frac{1}{X_C}(j{\omega }^2+j\omega \frac{R}{L}+\frac{1}{LC})$

Natural Response

$L\frac{dI}{dt}+IR+\frac{1}{C}\int Idt=0$

$\frac{dI}{dt}+I\frac{R}{L}+\frac{1}{LC}=0$

$\frac{d^{2}I}{d{t}^2}+\frac{R}{L}\frac{dI}{dt}+\frac{1}{LC}=0$

$s^2+\frac{R}{L}s+\frac{1}{LC}=0$

$s=-\alpha$ ± $\sqrt{{\alpha }^2-{\beta }^2}t$

$s=-\alpha \pm \lambda t$

$\alpha =\frac{R}{2L}$

$\beta =\frac{1}{LC}$

$\lambda =\sqrt{{\alpha }^2-{\beta }^2}t$

• $\lambda =0.{\alpha }^2={\beta }^2$ . There is only one real root,

s = -αt

$(\frac{R}{2L}{)}^2$ = $(\frac{1}{LC}{)}^2$

$R=\sqrt{\frac{L}{C}}$

$I=A{e}^{(}-\frac{t}{T})$

• ${\alpha }^2>{\beta }^2$ , There are two real roots,

$s=-\alpha$ ± $\sqrt{{\alpha }^2-{\beta }^2}$

$(\frac{R}{2L}{)}^2$ = $(\frac{1}{LC}{)}^2$

$R>\sqrt{\frac{L}{C}}$

$I=e^{-}\alpha t[e^{\lambda }t+e^{-}\lambda t]$

$I=ACos\lambda t$

$A=\frac{e^{-}\alpha t}{2}$

• ${\alpha }^2<{\beta }^2$ , There are two complex roots,

$s=-\alpha$ ± $\sqrt{{\alpha }^2-{\beta }^2}$

$(\frac{R}{2L}{)}^2$ = $(\frac{1}{LC}{)}^2$

$R>\sqrt{\frac{L}{C}}$

$I=e^{-}\alpha t[e^j\lambda t+e^{-}j\lambda t]$

$I=ASin\lambda t$

$A=\frac{e^{-}\alpha t}{2}$

Current change with time depends on the value of R L and C

$R=\sqrt{\frac{L}{C}}$ . Dòng điện giảm dần theo hàm số mủ của e

$R>\sqrt{\frac{L}{C}}$ . Dòng điện giảm đến một giá trị âm rồi tăng đến một giá trị dương

$R=\sqrt{\frac{L}{C}}$ . Mạch điện có có Dòng Điện của Sóng Sin giảm dần theo theo thời gian

Resonance Response

At resonance $Z_L-Z_C=0.V_C+V_L=0$

• $Z_L-Z_C=0$

$Z_L=Z_C$ .

$\omega L=\frac{1}{\omega C}$

$\omega =\sqrt{\frac{1}{LC}}$

Analyze the circuit at

$\omega =0.I=0$ . Capacitor opens circuit

$\omega =00.I=0$ . Inductor opens circuit

$\omega =\sqrt{\frac{1}{LC}}.I=\frac{V}{R}$ . $Z_L=Z_R.Z=Z_R+Z_L+Z_C=Z_R=R$

At resonance, series RLC is capable of select a bandwidth of frequencies where voltage is stable does not change with frequencies. Therefore, can be used as Tuned - Resonance Band Pas Selected Filter

Summary

• The natural Response of the RLC series is a second order differential equation of current

$\frac{d^{2}I}{dt}+\frac{R}{L}\frac{dI}{dt}+\frac{1}{LC}$

Depends on the value of Resistance the equation has

One Real Root	Two Real Roots	Two Complex Roots
One real root $R=\sqrt{\frac{L}{C}}$ $I=e^{-}\alpha t$	Two real roots $R>\sqrt{\frac{L}{C}}$ $I=e^{-}\alpha [e^{\lambda }t+e^{-}\lambda t]$ $I=ACos\lambda t$ $A=\frac{e^{-}\alpha t}{2}$	$R<\sqrt{\frac{L}{C}}$ $I=e^{-}\alpha [e^j\lambda t+e^{-}j\lambda t]<br><math>I=ASin\lambda t$ $A=\frac{e^{-}\alpha t}{2}$

• At Resonance when all the frequency dependent components cancel out RLC series behaves like Tuned Resonance Selected Band Pass Filter