Fractals/Mathematics/Roots

Finding roots of equation

Root

Names

• roots
• zeros
• solutions of the equations
• x-intercepts

Relation between roots and coefficients of the polynomial

• math.stackexchange question: parameter-plane-dynamics-of-fixed-points-and-their-preimages-for-standard-quadratic
• monodromy is the study of how objects behave as they "run round" a singularity

Methods

• Newton method
• "A useful way to visualize the roots of a complex function is to plot the 0 contours of the real and imaginary parts. That is, compute z = Dm(...) on a reasonably dense grid, and then use matplotlib's contour function to plot the contours where z.real is 0 and where z.imag is zero. The roots of the function are the points where these contours intersect." Warren Weckesser

Papers:

• A comparison of solution methods for Mandelbrot-like polynomials by Eunice Y. S. Chan

Programs:

• Free Online Polynomials root finder (factoring)
• gsl  : Example-programs-for-Multidimensional-Root-finding
• mpsolve
• Complex polynomial roots toy by Leo C. Stein
• Numerical computation of the roots of Mandelbrot polynomials: an experimental analysis by Dario A. Bini 2023

Examples

• 
  Example image with code showing importance of precision in solving equations

quadratic equation

The quadratic formula for the roots of the general quadratic equation

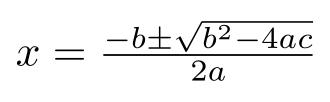
A quadratic equation (from the Latin quadratus for "square") is any equation having the form

$a{x}^2+bx+c=0$

where Template:Math represents an unknown, and Template:Math, Template:Math, and Template:Math represent known numbers such that Template:Math is not equal to Template:Math. If Template:Math, then the equation is linear, not quadratic. The numbers Template:Math, Template:Math, and Template:Math are the coefficients of the equation, and may be distinguished by calling them, respectively, the quadratic coefficient, the linear coefficient and the constant or free term.

Although the quadratic formula provides an exact solution, the result is not exact if real numbers are approximated during the computation, as usual in numerical analysis, where real numbers are approximated by floating point numbers (called "reals" in many programming languages). In this context, the quadratic formula is not completely numerical stable.

This occurs when :

• the roots have different order of magnitude, or, equivalently, when Template:Math and Template:Math are close in magnitude. In this case, the subtraction of two nearly equal numbers will cause loss of significance or catastrophic cancellation in the smaller root. To avoid this, the root that is smaller in magnitude, Template:Math, can be computed as $(c/a)/R$ where Template:Math is the root that is bigger in magnitude.
• a second form of cancellation can occur between the terms Template:Math and Template:Math of the discriminant, that is when the two roots are very close. This can lead to loss of up to half of correct significant figures in the roots.

When the term inside the square root (the "Discriminant") goes negative, i.e.

   if (b*b - 4*a*c < 0 ):

then doesn't have real roots, but have complex roots. ( see square root of negative number)

square root of Negative or complex number

If S is negative real numnber :

$\mathrm{Re}(S)<0$

$\mathrm{Im}(S)=0$

then its principal square root is

$\sqrt{S}=\sqrt{|S|}i.$

If S is a complex number : S = a+bi where a and b are real and b ≠ 0,

then its principal square root ( = the root with the non-negative real part) is :

$\sqrt{S}=\sqrt{\frac{|S|+a}{2}}+\mathrm{sgn}(b)\sqrt{\frac{|S|-a}{2}}i.$

where :

$|S|=\sqrt{a^2+b^2}$

is the absolute value (modulus) of S.

This can be verified by squaring the root.

See also

• How to analyze discrete dynamical system based on the map f  ?

References

• Geometry of polynomials and root-finding via path-lifting, February 2018 Nonlinearity 31(2):414-457 DOI: 10.1088/1361-6544 by Myong-Hi Kim, Marco Martens, Scott Sutherland