Introduction to Mathematical Physics/N body problem in quantum mechanics/Molecules
Vibrations of a spring model
We treat here a simple molecule model \index{molecule} to underline the importance of symmetry using \index{symmetry} in the study of molecules. Water molecule H0 belongs to point groups called . This group is compound by four symmetry operations: identity , rotation of angle , and two plane symmetries and with respect to two planes passing by the rotation axis of the operation (see figure figmoleceau).

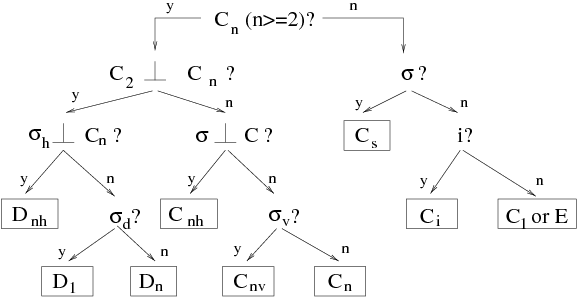
Group is one of the 32 possible point group (Template:IMP/citeTemplate:IMP/cite). Nomenclature is explained at figure ---figsymetr---.
each of these groups can be characterized by tables of "characters" that define possible irreducible representations \index{irreducible representation} for this group. Character table for group is:
Template:IMP/label Character group for group .}
| 1 | 1 | 1 | 1 | |
| 1 | 1 | -1 | -1 | |
| 1 | -1 | 1 | -1 | |
| 1 | -1 | -1 | 1 |
All the representations of group are one dimensional. There are four representations labelled , , and . In water molecule case, space in nine dimension . Indeed, each atom is represented by three coordinates. A representation corresponds here to the choice of a linear combination of vectors such that for each element of the symmetry group , one has: Template:IMP/eq Character table provides the trace, for each operation of the representation matrix . As all representations considered here are one dimensional, character is simply the (unique) eigenvalue of . Figure figmodesmol sketches the nine representations of group for water molecule. It can be seen that space spanned by the vectors can be shared into nine subspaces invariant by the operations . Introducing representation sum (Template:IMP/cite), considered representation can be written as a sum of irreducible representations:







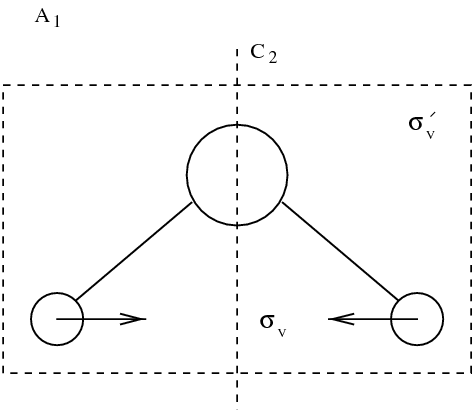
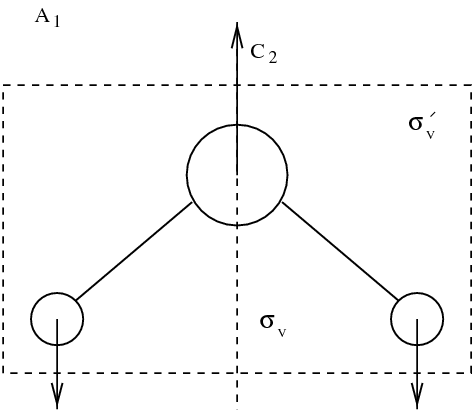
Eigenmodes of molecule. Vibrating modes are framed. Other modes correspond to rotations and translations.
It appears that among the nine modes, there are \index{mode} three translation modes, and three rotation modes. Those mode leave the distance between the atoms of the molecule unchanged. Three actual vibration modes are framed in figure figmodesmol. Dynamics is in general defined by:
where is the vector defining the state of the system in the basis. Dynamics is then diagonalized in the coordinate system corresponding to the three vibration modes. Here, symmetry consideration are sufficient to obtain the eigenvectors. Eigenvalues can then be quickly evaluated once numerical value of coefficients of are known.
Two nuclei, one electron
This case corresponds to the study of H molecule ([#References|references]). The Born-Oppenheimer approximation we use here consists in assuming that protons are fixed (movement of protons is slow with respect to movement of electrons). Template:IMP/rem The LCAO (Linear Combination of Atomic Orbitals) method we introduce here is a particular case of the variational method. It consists in approximating the electron wave function by a linear combination of the one electron wave functions of the atom\footnote{That is: the space of solution is approximated by the subspace spanned by the atom wave functions.}. Template:IMP/eq More precisely, let us choose as basis functions the functions and that are orbitals centred on atoms and respectively. This approximation becomes more valid as R is large (see figure figH2plusS).

Problem's symmetries yield to write eigenvectors as:
Notation using indices and is adopted, recalling the parity of the functions: for {\it gerade}, that means even in German and for {\it ungerade} that means odd in German. Figure figH2plusLCAO represents those two functions.


Taking into account the hamiltonian allows to rise the degeneracy of the energies as shown in diagram of figure figH2plusLCAOener.

N nuclei, n electrons
In this case, consideration of symmetries allow to find eigensubspaces that simplify the spectral problem. Those considerations are related to point groups representation theory. When atoms of a same molecule are located in a plane, this plane is a symmetry element. In the case of a linear molecule, any plane going along this line is also symmetry plane. Two types of orbitals are distinguished: Template:IMP/defn Template:IMP/defn Let us consider a linear molecule. For other example, please refer to ([#References|references]). Template:IMP/exmp Experimental study of molecules show that characteristics of bondings depend only slightly on on nature of other atoms. The problem is thus simplified in considering molecular orbital as being dicentric, that means located between two atoms. Those orbitals are called hybrids. Template:IMP/exmp