KS3 Computing/Binary

Binary

Binary (Base2) and Decimal (Base10)

When we count or measure something ourselves, we use the digits 0 to 9. Because there are ten digits we can use, this is Base10, usually called decimal (or sometimes denary).

A computer processor is made up of billions of switches, each of which, like a simple light switch, can be ON or OFF. We use 1s and 0s to represent the ONs and OFFs. Because there are only two possible values, we call this Base2, or Binary.

3-barrel combination lock

3-gang light switch

So we know that a lock with three dials, each with ten possible positions, give us a thousand combinations, and three switches with two possible positions give us eight combinations. But why is this?

With three columns, each with ten possibilities, the number of total combinations is 10 × 10 × 10, or 1000.

With three switches, each with two possibilities, the number of total combinations is 2 × 2 × 2, or 8.

For any number of dials and any number of positions on the dial, the number of possible combinations is always aᵇ, where a is the number of positions on the dial and b is the number of dials.

Bits and bytes

So now we know that binary is just a number system which uses the digits 0 and 1.

In computing, we call the number of switches or columns bits (this comes from binary digits.) So a number like 1011 we would say has 4 bits.

When you look at file sizes on your computer, you'll usually see them reported in these units:

bytes (B)
kilobytes (KB)	1 KB = 1024 B
megabytes (MB)	1 MB = 1024 KB = 1,048,576 B
gigabytes (GB)	1 GB = 1024 MB = 1,048,576 KB = 1,073,741,824 B

Why do we multiply by 1024...

...when kilo usually means multiply by a thousand (e.g. kilometers, kilogrammes)?

There are two answers to this question...

Easy answer: remember how we said that powers of two come up again and again in computing? Well, 1024 is Template:Math.

Harder answer: sometimes it isn't, sometimes it's 1000 after all. See Wikipedia's page about the Kilobyte. But don't worry about it too much, when your computer tells you how big a file is, its Kilobytes are 1024 bytes, its Megabytes are 1024 Kilobytes and so on.

Binary Numbers

When we learn to add or multiply in decimal, we use columns of (from right to left) Units, Tens, Hundreds, Thousands, and so on. The value of each column is ten times the column on its right.

Adding Hundreds, Tens and Units

(Needs a section here about converting Dec2Bin and Bin2Dec)

Counting in Binary

This counter shows how to count in binary from numbers zero through thirty-one.

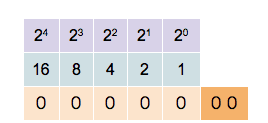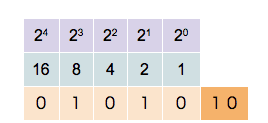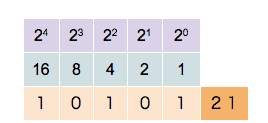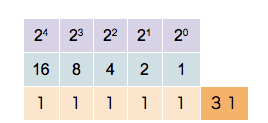
(Add a gif of counting in binary on one hand)

Activity: In groups of four, act out three-bit binary counter. Three people will be the bits, one person will need to direct.

1. Three people should sit in a row, in chairs - this represents 0 0 0.
2. To represent 0 0 1, the person on the right should stand up.
3. For 0 1 0 , the person on the right should sit down and the person in the middle should stand up.
4. Use the table from the first exercise to work through the values 0 to 7

What patterns do you notice? With practice, can your director join in so you become a four-bit counter?

(The person on the far right might want to swap places before their legs hurt from all the standing and sitting!)

Extension: Can you write an algorithm that anyone in the human binary counter could follow, regardless of how many digits there are, or which position they're in?

Sources and more reading

Some of the materials came from Wikipedia, however they may have been edited to suit the main audience of this book (Key Stage 3 pupils aged between 11 and 14)

• Wikipedia Binary Number article [Binary number]