Logic for Computer Scientists/Predicate Logic/SATCHMO

SATCHMO

The SATCHMO Theorem Prover was one of the first systems which used model generation, i.e. a bottom-up proof procedure. The prover was given by a small Prolog-program, which implements a tableau proof procedure. One restriction is that it requires range restricted formulae.

Definition 30

A first order clause $A_1\vee \cdots \vee A_n\leftarrow B_1\wedge \cdots \wedge B_m$ is called range restricted if every variable which occurs in the head $A_1\vee \cdots \vee A_n$ occurs in the body $B_1\wedge \cdots \wedge B_m$ as well.

1. Convert clauses to range restricted form:
   $q(x)\vee p(x,y)\leftarrow q(x)⇝q(X);p(X,Y)<-q(X),dom(Y)$
2. assert range-restricted clauses and dom clauses in Prolog database.
3. Call satisfiable:

kill satisfiable :-    assume(X) :- asserta(X).     
       (Head <- Body)            assume(X) :-  
       Body, not Head, !,          retract(X), !, fail.  
       component(HLit, Head),      component(E, (E ; _)).      
       assume(HLit),               component(E, (_ ; R)) :-    
       not false,                   !, component(E, R).   
       satisfiable.                component(E, E).  
  satisfiable.

First-Order completeness via Level-Saturation modification. This proof procedure implements Hyper Tableaux in the ground case.

Hyper Tableau - Ground Case

All open branches consist of positive literals only Take the following clause set as an example $\{\to A,\to B,A\wedge B\to C\vee D,A\wedge B\to E\vee D,A\wedge C\to \}$

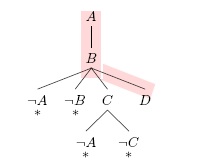
Definition 31 (Literal tree, Clausal Tableau)

A literal tree is a pair $(t,\lambda )$ consisting of a finite, ordered tree $t$ and a labeling function $\lambda$ that assigns a literal to every non-root node of $t$.

The successor sequence of a node $N$ in an ordered tree $t$ is the sequence of nodes with immediate predecessor $N$, in the order given by $t$.

A (clausal) tableau $T$ of a set of clauses $𝒮$ is a literal tree $(t,\lambda )$ in which, for every successor sequence $N_1,\dots ,N_n$ in $t$ labeled with literals $K_1,\dots ,K_n$, respectively, there is a substitution $\sigma$ and a clause $\{L_1,\dots ,L_n\}\in 𝒮$ with $K_i=L_i\sigma$ for every $1\le i\le n$. $\{K_1,\dots ,K_n\}$ is called a tableau clause and the elements of a tableau clause are called tableau literals.

Definition 32 (Branch, Open and Closed Tableau, Selection Function)

A branch of a tableau $T$ is a sequence $N_0,\dots ,N_n$ ($n\ge 0$) of nodes in $T$ such that $N_0$ is the root of $T$, $N_i$ is the immediate predecessor of $N_{i+1}$ for $0\le i<n$, and $N_n$ is a leaf of $T$. We say branch $b=N_0,\dots ,N_n$ is a prefix of branch $c$, written as $b\le c$ or $c\ge b$, iff $c=N_0,\dots ,N_n,N_{n+1},\dots ,N_{n+k}$ for some nodes $N_{n+1},\dots ,N_{n+k}$, $k\ge 0$. The branch literals of branch $b=N_0,\dots ,N_n$ are the set $lit(b)=\{\lambda (N_1),\dots \lambda (N_n)\}$. We find it convenient to use a branch in place where a literal set is required, and mean its branch literals. For instance, we will write expressions like $A\in b$ instead of $A\in lit(b)$.

In order to memorize the fact that a branch contains a contradiction, we allow to label a branch as either open or em closed. A tableau is closed if each of its branches is closed, otherwise it is open.

A selection function is a total function $f$ which maps an open tableau to one of its open branches. If $f(T)=b$ we also say that $b$ is selected in $T$ by $f$.

Note that branches are always finite, as tableaux are finite. Fortunately, there is no restriction on which selection function to use. For instance, one can use a selection function which always selects the "leftmost" branch.

Definition 33 (Hyper Tableau - Ground Case)

Let $S$ be a finite set of clauses and $f$ be a selection function. Hyper tableaux for $S$ are inductively defined as follows:
Initialization step: A one node literal tree is a hyper tableau for $S$. Its single branch is marked as "open".

Hyper extension step: If

1. $T$ is an open hyper tableau for $S$, $f(T)=b$ (i.e. $b$ is selected in $T$ by $f$) with open leaf node $N$, and
2. $C=A_1,\dots ,A_m\leftarrow B_1,\dots ,B_n$ is a clause from $S$ ($m\ge 0$, $n\ge 0$), called extending clause in this context, and
3. such that $\{B_1,\dots ,B_n\}\subseteq b$ (referred to as hyper condition)
   

then the literal tree $T^{\prime }$ is a hyper tableau for $S$, where $T^{\prime }$ is obtained from $T$ by attaching $m+n$ child nodes $M_1,\dots ,M_m,N_1,\dots ,N_n$ to $b$ with respective labels

$A_1,\dots ,A_m,\mathrm{\neg }{B}_1,\dots ,\mathrm{\neg }{B}_n$

and marking every new branch $(b,M_1),\dots ,(b,M_m)$ with positive leaf as "open", and marking every new branch $(b,N_1),\dots ,(b,N_n)$ with negative leaf as "closed".

Minimal Model Reasoning

The clause set $M=\{A\vee B\leftarrow ,B\leftarrow A\}$ obviously has two different models: $\{A,B\}$ and $\{B\}$. Under set inclusion these models can be compared and there are some tasks where it is appropriate to compute the (or in general a) smallest one. This is for example the case with

• Knowledge Representation, Circumscription
• Basis for default negation (GCWA)
• Applications: Deductive database updates, Diagnosis

There are basically two different methods to compute minimal models.

Minimal Model Reasoning – Niemel¨a’s Approach

Given a set of ground clauses $M$ the methods applies a model generating procedure, e.g. hyper tableau, which is able to generate all models.

Lemma 1: For every minimal model $p$ for $M$ there is a branch with literals $p$.

Assume that $\mathrm{\Sigma }$ is the set of atoms, which occur in the head of a clause from $M$, than the following Lemma holds.

Lemma 2: $p$ is a minimal model for $M$ iff $M\cup \{\mathrm{\neg }A\mid A\in \mathrm{\Sigma }\setminus p\}\models p$

This offers a general method: Generate model candidates, and test with Lemma 2.

$p=\{A,B\}$ is not a minimal model in our example from above, because $M\cup \{\}\models \{A,B\}$ iff $M\cup \{\leftarrow A\wedge B\}$ is unsatisfiable, which is not the case, hence $p$ does not correspond to a minimal model and hence the branch is closed.

$p=\{B\}$ is minimal because $M\cup \{\leftarrow A\}\models \{B\}$ iff $M\cup \{\leftarrow A\}\cup \{\leftarrow B\}$ is unsatisfiable. This is the case and hence $p$ is minimal and the branch remains open.

Properties: Soundness (by Lemma 2) Completeness (by Lemma 1), space efficiency.

Minimal Model Reasoning – Bry& Yayha‘s Approach

As an example we have the set $M=\{A\vee B\vee C\leftarrow ,B\leftarrow A,D\leftarrow B\}$

Lemma: With complement splitting, the leftmost open branch is a minimal model for $M$.

General method: Repeat: generate minimal model $p$, add $\leftarrow p$ to $M$. Properties: Soundness (by Lemma) Completeness as before, possibly exponentially many new clauses $\leftarrow p$.