Math for Non-Geeks/Absolute value and conjugation

{{#invoke:Math for Non-Geeks/Seite|oben}}

Absolute value of a complex number

Motivation of the absolute value

When dealing with real numbers, we introduced the absolute value function $|\cdot |:ℝ\to {ℝ}_{\ge 0}$, with which we could specify the distance of a certain number to zero. Visualised on the real number line this looks as follows:

absolute values of real numbers

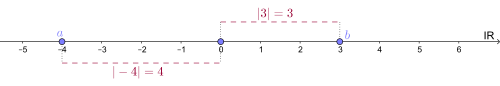
Also in the complex plane we can determine the distance of a complex number from the zero point. For this we use the theorem of Pythagoras. Let $z=a+b\mathrm{i}$ be a complex number:

The complex number z with its real part a and imaginary part b

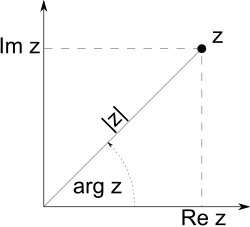
With the Pythagorean theorem, for the distance $|z|$ from zero, we have $|z{|}^2=\mathrm{Re}(z{)}^2+\mathrm{Im}(z{)}^2=a^2+b^2$. By taking roots on both sides, $|z|$ can be determined. There is:

The absolute value transfers some concepts of real numbers to the complex numbers. As $|x-y|$ in the real numbers is the distance between $x$ and $y$, so is $|z-w|$ in the complex numbers the distance between $z$ and $w$. The distance in turn can be used to define terms such as a limit: A complex number $z$ is the limit value of a sequence $(z_n{)}_{n\in \mathbb{N}}$ of complex numbers, if the distance $|z-z_n|$ between the limit value $z$ and the sequence elements $z_n$ becomes arbitrarily small (below any $ϵ$).

Complex conjugation

Motivation of the conjugation

The imaginary unit $\mathrm{i}$ as a root of $-1$ fulfils the equation ${\mathrm{i}}^2=-1$. We can imagine the multiplication $x\mapsto -1\cdot x$ as a $180^{\circ }$ rotation around the zero point. Now because of the equation ${\mathrm{i}}^2=-1$, the multiplication $x\mapsto -1\cdot x$ is the same as $x\mapsto \mathrm{i}\cdot (\mathrm{i}\cdot x)$. Thus, $x\mapsto \mathrm{i}\cdot x$ is an operation that corresponds to a $180^{\circ }$ rotation when used twice.

If a double multiplication with $\mathrm{i}$ corresponds to a $180^{\circ }$ rotation, then a single multiplication must correspond to a $90^{\circ }$ rotation. In particular, the imaginary unit $\mathrm{i}$ is equal to the number which results from a rotation of the number $1$ by $90^{\circ }$:

Rotation of the number 1 by 90° yields i

It is common in Mathematics to turn counter-clockwise. Thus, $\mathrm{i}$ is located where in $ℝ\times ℝ$ the $1$ lies on the $y$ axis. However, one could just as well have turned clockwise. Then the $\mathrm{i}$ would lie at the position of the $-1$ on the $x$ axis:

Rotation of the number 1 by -90° yields -i

We could also have derived the complex numbers from this alternative rotation. In that case we would have obtained a different set of complex numbers where the imaginary unit $\mathrm{i}$ is below the $x$ axis. In this alternative set of complex numbers the roles of $\mathrm{i}$ and $-\mathrm{i}$ are reversed. So if we swap $\mathrm{i}\leftrightarrow -\mathrm{i}$ everywhere, essential properties and structures obtained by number range expansion should be preserved. Such an interchange is shown in the figure:

In this figure, the imaginary part is multiplied by $-1$. This corresponds to a reflection of the complex number on the real ($x$) axis:

complex conjugation visualized

An example where this reflection is useful are the zeros of the function $f:ℂ\to ℂ,f(z)=z^2+1$. There is $f(\mathrm{i})={\mathrm{i}}^2+1=0$. Therefore $\mathrm{i}$ is a zero of $f$. On the other hand there is also $f(-\mathrm{i})=(-\mathrm{i}{)}^2+1=0$ and therefore $-\mathrm{i}$ is another zero. Let us consider $g(z)=z^2-2z+2$ with the zero $1+\mathrm{i}$. One might think that the negative of the number, $-1-\mathrm{i}$, is another zero. Unfortunately this is not the case. But if we exchange $\mathrm{i}$ with $\mathrm{-}i$, i.e. if we look at the complex number $1-\mathrm{i}$, we get another zero:

For die Nullstelle $z=a+b\mathrm{i}$ eines Polynoms scheint das an der reellen Achse gespiegelte $a-b\mathrm{i}$ eine weitere Nullstelle zu sein. Dies ist im Übrigen for all Polynome with rein reellen Koeffizienten der Fall. Dies weist darauf hin, dass die Abbildung $a+b\mathrm{i}\mapsto a-b\mathrm{i}$ eine Besondere ist. Diese Abbildung wird complex Konjugation genannt.

For the zero point $z=a+b\mathrm{i}$ of a polynomial, the $a-b\mathrm{i}$ mirrored on the real axis seems to be another zero point. This is the case for all polynomials with purely real coefficients. This indicates that the mapping $a+b\mathrm{i}\mapsto a-b\mathrm{i}$ might be particularly useful. As you progress with your math studies, you will see that it is useful in many more situations. So we better give it a name. Let's call it complex conjugation (since it connects/ conjugates $a+b\mathrm{i}$ and $a-b\mathrm{i}$).

Overview: Properties of the absolute value and the complex conjugation

Properties of the complex conjugation

For all $z$ and $w\in ℂ$ there is:

• $z=\bar{z}⟺\mathrm{Im}(z)=0⟺z\in ℝ$
• $\overline{\stackrel{‾}{w}}=w$
• $\overline{z+w}=\bar{z}+\bar{w}$
• $\overline{z\cdot w}=\bar{z}\cdot \bar{w}$
• $\overline{\sum _{k=1}^n{z}_k}=\sum _{k=1}^n\overline{z_k}$
• $\overline{\prod _{k=1}^n{z}_k}=\prod _{k=1}^n\overline{z_k}$
• $\text{Re}(w)=\frac{1}{2}\cdot (w+\bar{w})$
• $\text{Im}(w)=\frac{1}{2\mathrm{i}}\cdot (w-\bar{w})$
• $|z|=\sqrt{z\cdot \overline{z}}$
• $z^{-1}=\frac{\bar{z}}{|z{|}^2}$
• $\overline{\left(\frac{z}{w}\right)}=\frac{\bar{z}}{\bar{w}}$

Properties of the absolute value of a complex number

For all $z$ and $w\in ℂ$ there is:

• $|z|\ge 0$ and $|z|=0\iff z=0$ (positive definiteness)
• $|wz|=|w||z|$ (multiplicativity)
• $|\text{Re}(z)|\le |z|$ and $|\text{Im}(z)|\le |z|$
• $|w+z|\le |w|+|z|$ (triangle inequality)
• $|z|\le |\text{Re}(z)|+|\text{Im}(z)|$
• $||w|-|z||\le |w-z|$

Computation rules for complex conjugation

Compatibility of conjugation with finite sums and products

We know how the conjugation behaves with the sum and product of two numbers. What happens with sums and products with three or more numbers like $\overline{z_1+z_2+z_3}$? We use a trick: First, we consider $(z_1+z_2)$ as a single complex number. Then,we twice use the theorem of conjugation and sum:

There is also no difference for three summands if we first sum everything and then apply conjugation to the resulting number, or if we first conjugate every number and then sum everything. This is generally true for arbitrary sums and products of complex numbers, as we will prove below via induction.

Properties of the complex absolute funciton

Inverse triangle inequality

{{#invoke:Math for Non-Geeks/Seite|unten}}