Math for Non-Geeks/Cauchy sequences
{{#invoke:Math for Non-Geeks/Seite|oben}}
Motivation
In the last chapter, we learned about convergence of sequences . They were defined via the Epsilon-criterion, which says that must hold for all but finitely many . I.e. it holds for all with some . However, in order to apply this criterion, we need a candidate for the limit . What if we don't have such a candidate? Or more precisely,
A sequence converges, if the distance of to eventually tends to 0. In that case, also the difference between elements tends to 0. Conversely, if we know that goes to 0 if both and get large, then the amount of points where a possible limit or accumulation point might be shrinks together to a point. So the sequence should converge, then
The interesting question is now, what condition we have to put on and . If we just consider neighbouring sequence elements via setting , we might run into trouble: consider the sequence
This is a harmonic series. The difference of neighbouring elements is . But the sequence itself diverges to . We need a stronger criterion, i.e. we need to consider more pairs than just neighbours.
Derivation of Cauchy sequences
We try to get a condition on , which suffices for showing that a sequence converges. So let's take a sequence converging to and play a bit with it: The epsilon-definition of convergence reads
Template:Math We fix . Then, there is an index depending on with for all . What can we say about the difference for ? There is
So the triangle inequality for implies:
Sequence elements coming after are all separated by less than . Visually, all sequence elements are all situated inside the interval which has width :
The distance between two points in this interval is less than . So for a convergent sequence we have:
The , in here is a bit awkward to most mathematicians. They remove it by defining . The function is mapping bijectively onto . So instead saying "for all ", we could also use the term "for all ":
Sequences, which fulfil the above property are called Cauchy sequences . This definition does not require a limit . A sequence which converges, fulfils the above property, so any convergent sequence is a Cauchy sequence. But seeing that any Cauchy sequence converges is not so easy. Generally, this is even wrong: Not every Cauchy sequence converges! However, it is true that every Cauchy sequence in converges. In the rest this article , we successively construct a proof for this.
Math for Non-Geeks: Template:Hinweis
Definition of a Cauchy sequence
File:Zahlen - Quatematik.webm The definition for a Cauchy sequence reads: Math for Non-Geeks: Template:Definition
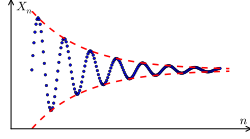
Intuitively, a sequence is Cauchy, if the difference between any two elements gets arbitrarily small as the element indices go to . Beware: it is a common mistake to think that only neighbouring elements must get close to each other. However, Cauchy sequences require all differences between elements to go to 0:
-
A Cauchy sequence: differences between two elements tend to 0.
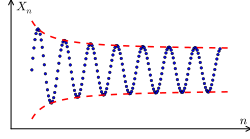
-
Not a Cauchy sequence: differences do not tend to 0.
Math for Non-Geeks: Template:Beispiel
Math for Non-Geeks: Template:Beispiel
Every convergent sequence is a Cauchy sequence
We essentially already proved this within the "derivation of Cauchy sequences". But it's always a good idea, to write down one's findings in a structured way. So let's do this:
Math for Non-Geeks: Template:Satz
Cauchy sequences are bounded
Convergent series are bounded. And we can prove the same for Cauchy sequences:
Math for Non-Geeks: Template:Satz
Cauchy sequences with convergent subsequences also converge
We would like to show that in , a Cauchy sequence converges. This is a somewhat longer task. So we first take a smaller step and prove the following smaller theorem:
Math for Non-Geeks: Template:Satz
Every Cauchy sequence converges
Now, that we have the smaller theorem above, we can use it to show the final theorem:
Math for Non-Geeks: Template:Satz
{{#invoke:Math for Non-Geeks/Seite|unten}}