Math for Non-Geeks/Superior and inferior limit

By limes superior and limes inferior, mathematicians denote the largest and the smallest accumulation point of a sequence. They are useful, if there are multiple limits and intuitively say what the "greatest limit" (limes superior) and the "smallest limit" (limes inferior) of that sequence are.

Motivation

We already learned about limits of a sequence. A limit is that unique number, to which a sequence tends. In every neighbourhood of the sequence, there are almost all elements, meaning only a finite number is allowed to be on the outside:

There are only finitely many elements outside the neighbourhood.

Sometimes, it seems like a sequence tends towards multiple numbers (like "multiple limits"). We also discussed that case: these numbers are then called "accumulation points" instead of "limits", since a limit must always be unique.

The set of accumulation points may be bounded or unbounded. In case it is bounded, there is a best upper and a best lower limit for the accumulation points, which we will call limes superior and limes inferior. Both are real numbers. Mathematically, for a sequence $(a_{n})_{n \in ℕ}$ we will denote the limes superior as $\underset{n \to \infty}{lim sup} a_{n}$ and the limes inferior as $\underset{n \to \infty}{lim inf} a_{n}$ .

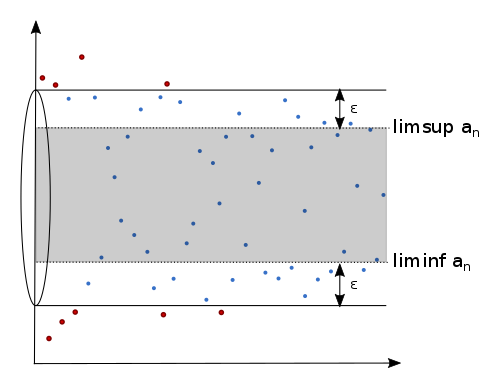
The closed interval $[\underset{n \to \infty}{lim inf} a_{n}, \underset{n \to \infty}{lim sup} a_{n}]$ then includes all accumulation points. We can even show that in any neighbourhood of this interval (i.e. a slightly bigger interval), there are almost all elements inside this neighbourhood. The following figure illustrates this situation for some $ϵ$ -neighbourhood $[\underset{n \to \infty}{lim inf} a_{n} - ϵ, \underset{n \to \infty}{lim sup} a_{n} + ϵ]$ around the original interval:

Definition

Now, let us turn to a mathematical description of "greatest and smallest accumulation point". We can directly define:

Math for Non-Geeks: Template:Definition

But: Does this definition even make sense? The accumulation points form a set. Those sets need not to have a maximum (greatest value) or minimum (smallest value), but might instead just have a supremum or infimum. Mathematicians wondered, when this is the case and soon found a surprising answer: The "awkward case" that there is no greatest/smallest limit does never occur! This statement ca actually be proven

Math for Non-Geeks: Template:Satz

This theorem establishes that the two definitions above actually make sense, so limes superior and limes inferior are well-defined.

Examples

Math for Non-Geeks: Template:Beispiel

limsup, liminf and limit

If limes superior and limes inferior of a sequence $(a_{n})_{n \in ℕ}$ exist and coincide, then the greatest and smallest accumulation point are identical, so there can only be one accumulation point. And the sequence cannot be unbounded, so it should converge to this one accumulation point. But does it actually do that? And does the converse hold true? I.e., if the sequence $(a_{n})_{n \in ℕ}$ converges, are limes superior and inferior identical? The answer turns out to be yes:

Math for Non-Geeks: Template:Satz

Math for Non-Geeks: Template:Hinweis

Math for Non-Geeks: Template:Aufgabe

Alternative characterization

In the literature, $\underset{n \to \infty}{lim sup} a_{n}$ and $\underset{n \to \infty}{lim inf} a_{n}$ are often defined in a different but equivalent way: Suppose, $(a_{n})_{n \in ℕ}$ is bounded. Then we have:

Math for Non-Geeks: Template:Satz Intuitively, the limes superior is the "smallest upper" and the limes inferior the "greatest lower bound" of $(a_{n})_{n \in ℕ}$ , as $n \to \infty$ . Or in other words: The bound is allowed to be violated by finitely many elements.