Math for Non-Geeks/ Derivatives

{{#invoke:Math for Non-Geeks/Seite|oben}} The derivative $f^{\prime }(x)$ is one of the central concepts within calculus. For a given function $f(x)$, the derivative $f^{\prime }(x)$ is another function which specifies the rate of change of $f(x)$ in $x$. It is used in various scientific disciplines, basically everywhere, where there is a "rate of change" within a dynamical system. Knowing about derivatives means having a powerful tool at hand: it allows you to describe and predict rates of change in a huge variety of applications.

Intuitions of the derivative

Te derivative is a mathematical object, which becomes useful in many situations. Depending on the situation, there are several intuitions which can make this abstract object come alive in your mind:

• Derivative as instantaneous rate of change: The derivative corresponds to what we intuitively understand as the rate of change of a function $f(x)$ at some instant $x$. A rate of change ($\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}$) describes how much a quantity changes ($\mathrm{\Delta }f$) in relation to the change of some reference quantity ($\mathrm{\Delta }x$). If we let ($\mathrm{\Delta }x$) run to 0, we get the rate of change within an "infinitely small amount of time". An example are speeds: Consider a given time-dependent position $s(t)$, i.e. the function $f$ is re-labeld as $s$ and $x$ is re-labelled as $t$. The quotient $\frac{\mathrm{\Delta }s}{\mathrm{\Delta }t}$ of "travelled distance" $\mathrm{\Delta }x$ and "elapsed time" $\mathrm{\Delta }t$ just describes the "average speed". In order to get the speed $v(t)$ at some time $t$, we make the time difference $\mathrm{\Delta }t$ smaller and smaller, such that the "average speed" $\frac{\mathrm{\Delta }s}{\mathrm{\Delta }t}$ goes over to an "instantaneous speed" $v(t)$ . This $v(t)$ is called first derivative and mathematicians write $v(t)=s^{\prime }(t)$ .
• Derivative as tangent slope: The derivative corresponds to the slope that the tangent of the graph has at the location of the derivative. Thus the derivative solves the geometric problem of determining the tangent to a graph by a point.
• Derivative as slope of the locally best linear approximation: Any function that has a derivative a point can be well approximated by a linear function in an environment around this point. The derivative corresponds to the slope of this linear function. This is useful if the function is hard to compute: the linear approximation can be computed way easier in many cases.
• Derivative as generalised slope: How steep is a given function? At first, the concept of the "slope of a function" is only defined for linear functions. But we can use the derivative to define the "slope" also for non-linear functions.

We will discuss these intuitions in detail in the following and use them to derive a formal definition of the derivative. We will also see that derivable functions are "kink-free", which is why they are also called smooth functions (think of smoothly bending some dough or tissue).

Derivative as rate of change

Introduction to the derivative

The derivative corresponds to the rate of change of a function $f$. How can this rate of change of a function be determined or defined? Let, for example be $f$ a real-valued function, which has the following graph:

The function f

For example, $f$ may describe a physical quantity in relation to another quantity. For example, $f(x)$ could correspond to the distance covered by an object at the time $x$. $f(x)$ could also be the air pressure at the altitude $x$ or the population size of a species at the time $x$. Now let us take the argument $\tilde{x}$, where the function has the function value $f(\tilde{x})$:

The function f with one argument and function value

Let us assume that $f(x)$ is the distance travelled by a car at the time $x$. Then the current rate of change of $f$ at the position $\tilde{x}$ is equal to the velocity of the car at the time $\tilde{x}$.

It is hard to determine the velocity directly with only $f(x)$ given. But we can estimate it. We take a point in time $x_1$ shortly after $\tilde{x}$ and look at the average speed in that time $v=\frac{\text{distance}}{\text{time}}$. The distance travelled in that time is $f(x_1)-f(\tilde{x})$, while the time difference is $x_1-\tilde{x}$. Thus the car has the average speed

This quotient, which indicates the average rate of change of the function $f$ in the interval $[\tilde{x},x_1]$, is called difference quotient. As its name suggests, it is a quotient of two differences. In the following figure we see that this difference quotient is equal to the slope of the secant passing through the points $(\tilde{x},f(\tilde{x}))$ and $(x_1,f(x_1))$:

The average rate of change corresponds to the slope of the secant.

This average speed is a good approximation of the current speed of our car at the time $\tilde{x}$. It is only an approximation since the movement of the car between $\tilde{x}$ and $x_1$ need not be uniform - it can accelerate or decelerate. But we should get a better result if we shorten the period for calculating the average speed. So let's look at a time $x_2$ which is even closer to $\tilde{x}$ and determine the average speed $\frac{f(x_2)-f(\tilde{x})}{x_2-\tilde{x}}$ for the new time interval between $\tilde{x}$ and $x_2$:

The secant for a point closer to the derivative argument

We can shorten the time difference even further by taking a sequence $(x_n{)}_{n\in \mathbb{N}}$ of times which converge towards $\tilde{x}$. For every $x_n$ we calculate the average speed $\frac{f(x_n)-f(\tilde{x})}{x_n-\tilde{x}}$ of the car in the period from $\tilde{x}$ to $x_n$. The shorter $x_n-\tilde{x}$, the less the car should be able to accelerate or decelerate in this period of time. So the average speed should converge to the current speed of the car at time $\tilde{x}$:

The secant slope (average rate of change) converges to the derivative (current rate of change).

Thus we have found a method to determine the current rate of change of $f$ at time $\tilde{x}$: We take any sequence of arguments $(x_n{)}_{n\in \mathbb{N}}$, which are all different from $\tilde{x}$ and for which $\underset{n\to \mathrm{\infty }}{\lim }{x}_n=\tilde{x}$. For every $x_n$ we determine the quotient $\frac{f(x_n)-f(\tilde{x})}{x_n-\tilde{x}}$. The current rate of change is the limit of these quotients:

The derivative or $f$ at $\tilde{x}$ is denoted as $f^{\prime }(\tilde{x})$. So we have the mathematical definition:

The limit of the difference quotient is sometimes also called differential quotient.

Negative time intervals

What happens if we do not choose $x_n$ in the future, but in the past of $\tilde{x}$? Let us draw this situation in a picture:

The average rate of change for an argument lower than the derivative argument

The average speed in the interval from $x_n$ to $\tilde{x}$ is then equal to $\frac{f(\tilde{x})-f(x_n)}{\tilde{x}-x_n}$. If we extend this fraction by a factor of $-1$, we get

We get the same term as in the previous section. This gives the average speed, no matter if $x_n<\tilde{x}$ or $x_n>\tilde{x}$. Thus, in the case of a negative time interval with $x_n<\tilde{x}$ the average speed should also be close to the current speed of the car at the time $\tilde{x}$, if $x_n$ is only sufficiently close to $\tilde{x}$. There is

where $(x_n{)}_{n\in \mathbb{N}}$ is any sequence of different from $\tilde{x}$ with $\underset{n\to \mathrm{\infty }}{\lim }{x}_n=\tilde{x}$. The sequence elements of $(x_n{)}_{n\in \in \mathbb{N}}$ can sometimes be larger and sometimes smaller than $\tilde{x}$ depending on the index $n$:

A sequence of secants for computing the derivative

Refining the definition

Let now $f:D\to ℝ$ be a real-valued function and let $\tilde{x}\in D$. As we have seen above, there is

where ${\left(x_n\right)}_{n\in \mathbb{N}}$ is a sequence of arguments different from $\tilde{x}$ which converges to $\tilde{x}$. In order to have at least one such sequence of arguments, $\tilde{x}$ must be an accumulation point of the domain $D$ (an element is an accumulation point of a set exactly when there is a sequence not including that number but converging towards it). This may sound more complicated than it often is. In most cases $D\subseteq ℝ$ is an interval and then every $\tilde{x}\in D$ is an accumulation point of $D$. For the definition of the differential quotient it should not matter which sequence $(x_n{)}_{n\in \mathbb{N}}$ we choose. Accordingly, we can define the derivative:

We can shorten this definition by using limits for functions. As a reminder: There is according to definition: $\underset{x\to c}{\lim }g(x)=L$ if and only if $\underset{n\to \mathrm{\infty }}{\lim }g(x_n)=L$ for all sequences $(x_n{)}_{n\in \mathbb{N}}$ of arguments non-equal to $c$ with $\underset{n\to \mathrm{\infty }}{\lim }{x}_n=c$. So:

The h-method

Definition of the derivative via the h-method: For the respective h-values the corresponding secants are drawn in. You see that for $h\to 0$ the secant changes into the tangent and thus the secant slope (difference quotients) changes into the tangent slope (derivative).

There is an equivalent option to define the derivative. For this we go from the differential quotient $\underset{x\to \tilde{x}}{\lim }\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ and perform the substitution $x=\tilde{x}+h$. The new variable $h$ just describes the difference between $\tilde{x}$ and the point where the difference quotient is formed. For $x\to \tilde{x}$, equivalently goes $h\to 0$. So we can also define the derivative as follows

Applications in science and technology

We have come to know the derivative as the current rate of change of a quantity. As such, it occurs frequently in science or applications. Several variables are defined as rates of change, for example:

• velocity: The velocity is the instantaneous rate of change of the distance travelled by an object.
• Acceleration: The acceleration is the instantaneous rate of change of the speed of an object.
• Pressure change: Let $p(h)$ the air pressure at altitude $h$. The derivative $p^{\prime }(h)$ is the rate of change of air pressure with altitude. This example shows that the rate of change need not always be related to time. It can also be the rate of change with respect to another quantity, e.g. altitude.
• Chemical reaction rate: Let's consider a chemical reaction $A\to B$. Let $d_A(t)$ the concentration of the substance $A$ at time $t$. The derivative ${d_A}^{\prime }(t)$ is the instantaneous rate of change of the concentration of $A$ and thus indicates how much of the substance $A$ is converted into the substance $B$. Thus ${d_A}^{\prime }(t)$ indicates the chemical reaction rate for the reaction $A\to B$.
• Often the number of individuals $N(t)$ in a population is considered (for example the number of people on the planet, the number of bacteria in a Petri dish, the number of animals of a species or the number of atoms of a radioactive substance). The derivative $N^{\prime }(t)$ represents the instantaneous rate of change of individuals at the time $t$.

Definitions

Difference quotient and differential quotient

The terms "difference quotient" and "differential quotient" are mathematically defined as follows:

Derivative function

The derivative function assigns to every argument $x$ of the function $f$ its derivative $f^{\prime }(x)$. Within the animation, the derivative function is evaluated at several arguments. It corresponds to the slope of the tangent at those points.

If a function $f:D\to ℝ$ with $D\subseteq ℝ$ is differentiable at every point within its domain of definition, then $f$ has a derivative at every point in $D$. The function that assigns its derivative $f^{\prime }(\tilde{x})$ to every m argument $\tilde{x}$ is called derivative function of $f$:

Notations

Historically, different notations have been developed to represent the derivative of a function. In this article we have only learned about the notation $f^{\prime }$ for the derivative of $f$. It goes back to the mathematician Joseph-Louis Lagrange , who introduced it in 1797. Within this notation the second derivative of $f$ is denoted $f^{″}$ and the $n$-th derivative is denoted $f^{(n)}$ .

Isaac Newton - (the founder of differential calculus besides Leibniz) - denoted the first derivative of $x$ with $\dot{x}$, accordingly he denoted the second derivative by $\ddot{x}$. Nowadays this notation is mainly used in physics for the derivative with respect to time.

Gottfried Wilhelm Leibniz introduced for the first derivative of $f$ with respect to the variable $x$ the notation $\frac{\mathrm{d}f}{\mathrm{d}x}(x)$. This notation is read as "d f over d x of x". The second derivative is then denoted $\frac{{\mathrm{d}}^{2}f}{\mathrm{d}{x}^2}(x)$ and the $n$-th derivative is written as $\frac{{\mathrm{d}}^{n}f}{\mathrm{d}{x}^n}(x)$.

The notation of Leibniz is mathematically speaking not a fraction! The symbols $\mathrm{d}f$ and $\mathrm{d}x$ are called differentials, but in modern calculus (apart from the theory of so-called "differential forms") they have only a symbolic meaning. They are only allowed in this notation as formal differential quotients. Now there are applications of derivatives (like the "chain rule" or "integration by substitution"), in which the differentials $\mathrm{d}f$ or $\mathrm{d}x$ can be handled as if they were ordinary variables and in which one can come to correct solutions. But since there are no differentials in modern calculus, such calculations are not mathematically correct.

The notation $Df$ or $D_{x}f(x)$ for the first derivative of $f$ dates back to Leonhard Euler. In this notation, the second derivative is written as $D^{2}f$ or $D_x^{2}f(x)$ and the $n$-th derivative as $D^{n}f$ or $D_x^{n}f(x)$.

Overview about notations

Notation of the …	1st derivative	2nd derivative	$n$-th derivative
Lagrange	$f^{\prime }$	$f^{″}$	$f^{(n)}$
Newton	$\dot{f}$	$\ddot{f}$	$\stackrel{n}{\dot{f}}$
Leibniz	$\frac{\mathrm{d}f}{\mathrm{d}x}$	$\frac{{\mathrm{d}}^{2}f}{\mathrm{d}{x}^2}$	$\frac{{\mathrm{d}}^{n}f}{\mathrm{d}{x}^n}$
Euler	$Df$	$D^{2}f$	$D^{n}f$

Derivative as tangential slope

For $\mathrm{\Delta }x=x-\tilde{x}\to 0$ the secant slope $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ converges to the tangential slope. The derivative $f^{\prime }(\tilde{x})$ is equal to the tangent slope of the tangent touching the graph at the point $(\tilde{x},f(\tilde{x}))$.

If a differentiable function is used, a tangent can be fitted to it at every m point of the graph. The derivative corresponds to the slope of this tangent.

The derivative $f^{\prime }(\tilde{x})$ corresponds to the limit value $\underset{x\to \tilde{x}}{\lim }\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$. The difference quotient $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ is the slope of the secant between the points $(\tilde{x},f(\tilde{x}))$ and $(x,f(x))$. In the case of the boundary value formation $x\to \tilde{x}$, this secant merges into the tangent that touches the graph of $f$ at the point $(\tilde{x},f(\tilde{x}))$:

function with a secant and a tangent

Damit ist die derivative $f^{\prime }(\tilde{x})$ gleich der Steigung der Tangente am Graphen durch den Punkt $(\tilde{x},f(\tilde{x}))$. Die derivative kann also genutzt werden, um die Tangente an einem Graphen zu bestimmen. Somit löst sie auch ein geometrisches Problem. Mit $f^{\prime }(\tilde{x})$ kennen wir die Steigung der Tangente and with $(\tilde{x},f(\tilde{x}))$ einen Punkt auf der Tangente. Damit können wir die functionsgleichung dieser Tangente bestimmen.

Thus the derivative $f^{\prime }(\tilde{x})$ is equal to the slope of the tangent to the graph through the point $(\tilde{x},f(\tilde{x}))$. we may also use the derivative to compute the tangent to a graph. With $f^{\prime }(\tilde{x})$ we know the slope of the tangent. The offset can be determined using that $(\tilde{x},f(\tilde{x}))$ is a point on the tangent. The following question illustrates how this works:

Derivative as characterization of best approximations

Approximating a differentiable function

The derivative can be used to approximate a function. One may even define the derivative as the "best linear approximation" to a function. To find this approximation we start with the definition of the derivative as a limit:

The difference quotient $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ gets arbitrarily close to the derivative $f^{\prime }(\tilde{x})$, if $x$ gets sufficiently close to $\tilde{x}$. For $x\approx \tilde{x}$ we can write:

In the following we assume, that the expression $x\approx \tilde{x}$ for "$x$ is approximately as large as $\tilde{x}$" is well defined and obeys the common arithmetic laws for equations. So we can change this equation to

If $x$ is sufficiently close to $\tilde{x}$, then $f(x)$ is approximately equal to $f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$. This value can thus be used as an approximation of $f(x)$ near the derivative position. The function with the assignment rule $x\mapsto f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$ is a linear function, since $\tilde{x}$ is an arbitrary but fixed point.

The assignment rule $t(x)=f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$ describes the tangent, which touches the graph of the function at the position where the derivative is taken. Thus, the tangent near the point of contact is a good approximation of the graph. This is also shown in the following diagram. If one zooms in close enough at a point in a differential function, the graph looks approximately like a straight line:

Differentiable functions locally look like a line

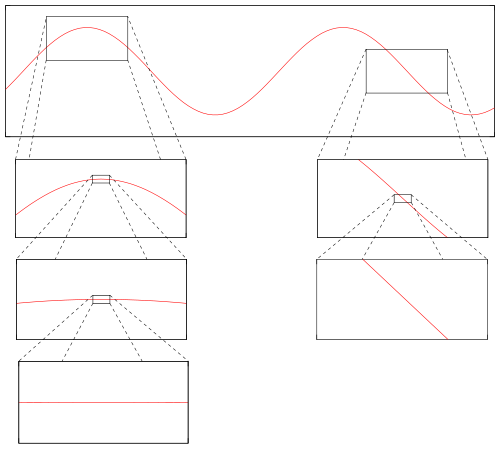
This line is described by the assignment rule $t(x)=f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$ and corresponds to the tangent of the graph at this position.

Example: The sine for small angles

Let's take a look at the above mentioned example. For this we consider the sine function $\sin (x)$. Its graph is

The graph of a sine function

As we shall see, the derivative of the sine is the cosine and thus

the linear approximation of the sine is hence

In the vicinity of zero, there is $\sin (x)\approx x$. This is the so called small-angle approximation. Thus, $\sin \left(\frac{1}{4}\right)$ can be approximated by $\frac{1}{4}$. With $\sin \left(\frac{1}{4}\right)=0.2474\dots$ this approximation is also quite good. The following diagram shows that near zero, the sine function can be described approximately by a line $\sin (x)\approx x$:

Small-angle approximation for the sine function

The diagram also shows that this approximation is only good near the derivative point. For values $x$ far away from zero, $\sin (x)$ differs greatly from $x$. The approximation $\sin (x)\approx x$ is therefore only meaningful for small arguments!

Quality of approximations

How good is the approximation $f(x)\approx f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$? To answer this, let $ϵ(x)$ be the value with

The value $ϵ(x)$ is therefore the difference between the difference quotient $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ and the derivative $f^{\prime }(\tilde{x})$. This difference disappears in the limit $x\to \tilde{x}$, because for this limit the difference quotient turns into a differential quotient, i.e. the derivative $f^{\prime }(\tilde{x})$. There is also $\underset{x\to \tilde{x}}{\lim }ϵ(x)=0$. Now we can rearrange the above equation and get

The error between $f(x)$ and $f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$ is thus equal to the term $\delta (x)=ϵ(x)\cdot (x-\tilde{x})$. Because of $\underset{x\to \tilde{x}}{\lim }ϵ(x)=0$ there is

So the error $\delta (x)$ disappears for $x\to \tilde{x}$. But we can say even more: $\delta (x)$ decreases faster than a linear term towards zero. Even if we divide $\delta (x)$ by $x-\tilde{x}$ and thus greatly increase this term near $\tilde{x}$, then $\frac{\delta (x)}{x-\tilde{x}}$ disappears for $x\to \tilde{x}$. There is

The error $\delta (x)$ in the approximation $f(x)\approx f(\tilde{x})+f^{\prime }(\tilde{x})\cdot (x-\tilde{x})$ thus falls off to zero faster than linear for $x\to \tilde{x}$. Let us summarize the previous argumentation in one theorem:

Alternative definition of the derivative

The fact that differentiable functions can be approximated by linear functions characterises the derivative. Every function $f$ is differentiable at the position $\tilde{x}$, if a real number $c\in ℝ$ (best approximation parameter) as well as a function $\delta$ exist, such that that $f(x)=f(\tilde{x})+c\cdot (x-\tilde{x})+\delta (x)$ and $\underset{x\to \tilde{x}}{\lim }\frac{\delta (x)}{x-\tilde{x}}=0$ apply. Its derivative is then $f^{\prime }(\tilde{x})=c$. There is

So we can also define the derivative as follows:

Describing derivatives using a continuous function

There is a further characterisation of derivative. We start with the formula

Where $ϵ(x)$ is the difference between the difference quotient and the derivative (which disappears for $x\to \tilde{x}$). If we rearrange this formula we get:

Template:Math

The function $\phi (x)$ for $x\to \tilde{x}$ has the property

Thus $\phi (x)$ can be extended to a function which is continuous at the position $\tilde{x}$, whereby the function value is set $\phi (\tilde{x})=f^{\prime }(\tilde{x})$. This representation of a differentiable function allows a further characterisation of continuous functions:

Derivative as generalized slope

The slope of a linear function is given by the quotient $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{y_2-y_1}{x_2-x_1}$.

The slope is initially only defined for linear functions $g$ with the assignment rule $g(x)=mx+b$ where $m,b\in ℝ$. For such functions the slope is equal to the value $m$ and can be calculated using the difference quotient. For two different arguments $x$ and $\tilde{x}$ from the domain of definition $g$ there is:

Now $m$ is also the derivative of $g$ at every accumulation point $\tilde{x}$ of the domain of definition:

The derivative of a linear function is therefore always equal to its slope. But the derivative is more general: it is defined for all differentiable functions. (Remember: A term $A$ is a generalisation of another term $B$, if $A$ is the same as $B$ in all cases where $B$ is defined and $A$ can be applied to other cases.)

So we can consider the derivative as the slope of a function at a point. The transition slope $\to$ derivative thus changes from a global property (the slope for linear functions is defined for the whole function), to a local property (the derivative is the instantaneous rate of change of a function).

Left-hand and right-hand derivative

Definition

The derivative of a function $f:D\to ℝ$ is the limit of the difference quotient $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ for $x\to \tilde{x}$. The difference quotient can be understood as a function $D\setminus \{\tilde{x}\}\to ℝ$, which is defined for all $x\in D$ except for $x=\tilde{x}$. So $\underset{x\to \tilde{x}}{\lim }\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ is actually the limit value of a function.

The terms "Left-hand and right-hand derivative" can also be considered for the difference quotient. Thus we obtain the terms "left-hand" and "right-hand" derivative. For the left-hand derivative, only secants to the left of the considered point are evaluated. So only difference quotients $\frac{f(x)-f(\tilde{x})}{x-\tilde{x}}$ are considered, where $xis<\tilde{x}$. Then it is checked whether the difference quotient converges to a number in the limit $x\to \tilde{x}$ converge against a number. If the answer is yes, then this number is the left-hand derivative at that point:

Here $f_{-}\text{'}(\tilde{x})$ is the notation for the left-hand derivative of $f$ at the position $\tilde{x}$. For this limit to make sense, there must be at least one sequence $(x_n{)}_{n\in \mathbb{N}}$ of arguments that converges from the left towards $\tilde{x}$. So $\tilde{x}$ has to be an accumulation point of the set $D\cap (-\mathrm{\infty },\tilde{x})=\{x\in D:x<\tilde{x}\}$.

Analogously, the right-hand derivative can be defined as follows:

functions only have a limit value at one position in their domain of definition if both the left-hand and the right-hand limit value exist at this position and both limit values match. We can apply this theorem directly to derivative functions:

Example

We have already shown that the absolute value function $f:ℝ\to ℝ:x\mapsto |x|$ is not differentiable at $\tilde{x}=0$. However, we can still show that the right-hand derivative exists at this position and is equal to $1$:

Analogously, we can show that the left-hand derivative is equal to $-1$ at this position:

Since the right-hand and left-hand derivatives do not coincide, the absolute value function cannot be differentiated at $\tilde{x}=0$. At this point, it has left-hand and right-hand derivatives, but no general derivative.

Weil die rechtsseitige and die linksseitige derivative nicht übereinstimmen, ist die Betragsfunktion an der Stelle $\tilde{x}=0$ nicht ableitbar. Sie besitzt dort zwar links- and rechtsseitige derivativeen, aber keine derivative.

Differentiable functions do not have kinks

In the above example we have seen that the absolute value function is not differentiable. This is because the absolute value function "has a kink" at the position $\xi =0$, so that the left-hand and right-hand derivative are different. If we go to $\xi =0$ from the left-hand side, the derivative is equal to $-1$, while the derivative from the right-hand side is equal to $1$. The kink in the absolute value function thus prevents differentiability.

So if a function has a kink, it is not differentiable at this point. In other words: differentiable functions are kink-free. Therefore they are also called smooth functions (actually, smooth means "infinitely many times differentiable"). This does not mean, however, that kink-free functions are automatically differentiable. As an example, let us consider the sign function $\mathrm{sgn}(x)$ with the definition

Its graph is

Graph of the sign function

This function is not differentiable at the zero point $\tilde{x}=0$, because near the the "jump" of the function, the difference quotient converges towards infinity. For the right-hand derivative there is for example:

The sign function has no kink at the zero point. Instead, it makes a "jump" there.

At the example of the sign function we see that being "free of kinks" and "differentiable" cannot be the same. However, freedom from kinks is a prerequisite for differentiability. So differentiable functions are free of kinks.

Relations between differentiability, continuity and continuous differentiability

Continuous differentiability of a function $f$ implies its differentiability, which in turn implies its continuity. The converse statements do not hold, as we will see in the course of this section:

The first implication follows directly from the definition: A function $f$ is called continuously differentiable if it is differentiable and the derivative function $f^{\prime }$ is continuous. Thus, continuously differentiable functions are also differentiable. The second implication needs some more work:

Differentiable functions are continuous

We now show that every at one point differentiable function is also continuous at this point. Thus, differentiability is a stronger condition for a function than continuity:

Application: Non-continuous functions are not differentiable

From the previous section we know that every differentiable function is continuous:

Applying the principle of contraposition to this implication, we also get:

Example: Non-continuous functions are not differentiable

Take, as an for example the sign function

It is not continuous at $\tilde{x}=0$. So it is also not differentiable there. We can prove non-continuity by taking a sequence $x_n=\frac{1}{n}$. This sequence converges towards zero. If the sign function was differentiable, then the limit value $\underset{n\to \mathrm{\infty }}{\lim }\frac{f(x_n)-f(0)}{x_n-0}$ would have to exist. However

The limit value does not exist in $ℝ$. Therefore the sign function is - as expected - not differentiable at $\tilde{x}=0$.

Not every differentiable function is continuously differentiable

In the following example, we already use some derivatives rules, which will be discussed in more detail in the next chapter. Perhaps you already know them from school. If not, they are a useful insight to what will follow.

Exercises

Criterion for differentiability

{{#invoke:Math for Non-Geeks/Seite|unten|quellen=

• Abschnitt Notationen des Wikipedia-Artikels „Differentialrechnungen“, abgerufen am 7. August 2016. Autorinnen and Autoren dieses Abschnitts sind unter anderem Benutzer:Christian1985, Benutzer:Roomsixhu, Benutzer:FranzR, Benutzer:DerSpezialist and Benutzer:SaltzGurke. Dieser Abschnitt steht unter einer CC-BY-SA 3.0 Lizenz.
• Abschnitt Example des Wikipedia-Artikels Derivative, abgerufen am 14.08.2016. Dieser Abschnitt steht unter einer CC-BY-SA 3.0 Lizenz.
• Greefrath, G., Oldenburg, R., Siller, H. S., Ulm, V., & Weigand, H. G. (2016). Aspects and "Grundvorstellungen" of the Concepts of Derivative and Integral. Journal für Mathematik-Didaktik, 37(1), 99-129.

}}