Physics Exercises/Electrostatics

Electric field superposition principle

1. In words, and by equation, state the principle of superposition for electric fields.

Figure illustrating superposition principle.

In physics, the electric field superposition principle postulates that, for all linear systems, the net response at a given place and time caused by two or more charges is the sum of the responses which would have been caused by each charge individually.

Mathematically that can be written:

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2+{\overrightarrow{E}}_3+...+{\overrightarrow{E}}_n=\sum _{i=1}^n{\overrightarrow{E}}_i=\sum _{i=1}^n\frac{1}{4\pi {ϵ}_0{r}^2}{\overrightarrow{u_r}}_i$

Note that this is a vector equation. Hence one must add the components using vector rules.

Finding the electric field associated with a dipole

1. An electric dipole is matched, equal but opposite, charges separated by a fixed distance. Find the electric field associated with an electric dipole. Perform this for three cases:

a. Find the electric field perpendicular to the axis between dipole charges. Find the far field approximation.

b. Find the electric field along the axis of the dipole charges. Compare the far field approximation for this case with that of a) above.

c. Find the electric field perpendicular in a plane which includes the dipole charges

A w:water molecule. A molecule of water has an electric moment because of the unequal sharing of its electrons in a "bent" structure. A separation of charge is present with negative charge in the middle (red shade), and positive charge at the ends (blue shade).

In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity. It is important in understanding practical matters like the construction of a capacitor.

Finding the electric field perpendicular to the axis between dipole charges

Figure 1: An electric dipole

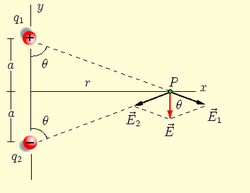
To determine the electric field which result from the dipole charges in Figure 1 that are separated by a distance 2a, we simply sum the fields from each charge individually. Note that the fields are vectors.

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2$

The distance of each charge (r) from the point where the electric field is measured is:

$r=\sqrt{a^2+x^2}$

The magnitude of the electric field (E₁) due to the first charge (q₁) and the magnitude of the electric field (E₂) due to the second charge (q₂) are the same although the directions are different.

$E_1=E_2=\frac{1}{4\pi {ϵ}_0}\frac{q}{r^2}=\frac{1}{4\pi {ϵ}_0}\frac{q}{a^2+x^2}$

The components of the electric field along the x axis $E_{1_x}$ and $E_{2_x}$ have the same magnitude but opposite directions and cancel each other out.

$E_{1_x}+E_{2_x}=0$

As a result of this the horizontal components of the electric field vectors cancelling is that summing ${\overrightarrow{E}}_1$ and ${\overrightarrow{E}}_2$ reduces to summing $E_{1_y}$ and $E_{2_y}$. Further, the magnitude of the vertical components are identical, $E_{1_y}=E_{2_y}$. Since $\cos \theta =\frac{adjacent}{hypotenuse}$ finding the vertical component reduces to:

$E_{1_y}=E_{2_y}=E_1\cos \theta$ or :$E_y=2E_1\cos \theta$

But we also know that:

$\cos \theta =\frac{a}{\sqrt{a^2+x^2}}$

So we can substitute this into the equation for $E$ which yields:

$E=2E_1\cos \theta =\frac{2}{4\pi {ϵ}_o}\frac{q}{a^2+x^2}\frac{a}{\sqrt{a^2+x^2}}=\frac{1}{4\pi {ϵ}_o}\frac{2aq}{(a^2+x^2{)}^{\frac{3}{2}}}$

In the region distant from the dipole x is much greater than a (x>>a). This is commonly referred to as the "far field" region. We can find how the field behaves in the far field region by factoring out x.

$E=\frac{1}{4\pi {ϵ}_o}\frac{2qa}{(a^2+x^2{)}^{\frac{3}{2}}}=\frac{1}{4\pi {ϵ}_o}\frac{2qa}{x^3}\frac{1}{(1+{(\frac{a}{x})}^2{)}^{\frac{3}{2}}}$

By inspection we can conclude that when x>>a then this approaches

$E\approx \frac{1}{4\pi {ϵ}_o}\frac{2qa}{x^3}$

An important question for some analyses might be: over what range is the far field approximation valid? We can find out by using a binomial expansion (review of binomial expansion immediately below this section if you need it).

$E=\frac{1}{4\pi {ϵ}_o}\frac{2qa}{(a^2+x^2{)}^{\frac{3}{2}}}=\frac{1}{4\pi {ϵ}_o}\frac{2qa}{x^3}\frac{1}{(1+{(\frac{a}{x})}^2{)}^{\frac{3}{2}}}$

Where we will expand

$\frac{1}{(1+{(\frac{a}{x})}^2{)}^{\frac{3}{2}}}$$=(1+{(\frac{a}{x})}^2{)}^{-\frac{3}{2}}=1-\frac{3}{2}{(\frac{a}{x})}^2+...$

If you want to use the approximation only when it introduces an error less than 1%, then - since the first term is unity, you want the second term to be less than 1/100th of unity, or:

$\frac{1}{100}>\frac{3}{2}{\left(\frac{a}{x}\right)}^2$

$\frac{2}{300}>{\left(\frac{a}{x}\right)}^2$

$\sqrt{\frac{2}{300}}>\left(\frac{a}{x}\right)$

$x>\sqrt{150}\cdot a$

So if x is 12.3 times larger than a, this approximation is valid within 1%.

Binomial expansion review

Review of the binomial expansion:

$\mathbf{(}\mathrm{𝟏}\mathbf{+}𝐚{\mathbf{)}}^{𝐧}=1+\frac{n}{1!}\cdot a+\frac{n(n-1)}{2!}\cdot a^2+\frac{n(n-1)(n-2)}{3!}\cdot a^3+...$

$\mathbf{(}\mathrm{𝟏}\mathbf{+}𝐚{\mathbf{)}}^{\mathbf{-}\frac{3}{2}}=1+\frac{1}{1!}\cdot \frac{-3}{2}\cdot a+\frac{1}{2!}\cdot \frac{-3}{2}\cdot \frac{-5}{2}\cdot a^2+\frac{1}{3!}\cdot \frac{-3}{2}\cdot \frac{-5}{2}\cdot \frac{-7}{2}\cdot a^3+...$

informal source link

Finding the electric field along the axis formed by dipole charges

Figure 2 - the layout for calculating the electric field along the line through the dipole charges.

The net electric field is the sum of the contributions to the electric field from the dipole charges.

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2$

The first thing one always should do when solving a problem is to consider what you know by simple inspection. In this case the magnitude and layout of the charges tells use several things. Since they are equal and we know that the electric field from a point charge falls off as 1 over r² then we know that the nearest charge will always dominate. Further we also know that along the axis that we're calculating the electric field there will be no vertical component of the electric field.

$E_{1_y}=E_{2_y}=0$

So now we will calculate the magnitude of the electric field from each in the x direction: $E_{1_x}$ and $E_{2_x}$.

$E_1=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r-a)}^2}{E}_2=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(r+a)}^2}$

Adding the vector magnitudes $E_{1_x}$ and $E_{2_x}$

$E=E_{1_x}+E_{1_x}$

And substituting in the equations above yields:

$E=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r-a)}^2}+\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(r+a)}^2}=\frac{1}{4\pi {ϵ}_0}[\frac{q}{{(r-a)}^2}-\frac{q}{{(r+a)}^2}]=\frac{1}{4\pi {ϵ}_0}4aq\frac{r}{{(r^2-a^2)}^2}$

The quantity 2qa is defined as the dipole moment (p) and so we can substitute:

$p=2qa$

With that substitution we now get:

$E=\frac{1}{2\pi {ϵ}_0}\frac{pr}{{(r^2-a^2)}^2}$

Consider the far field case (i.e., the case where $r$ >> $a$)

Then one can see that $r^2$ >> $a^2$ and that $r^2-a^2$ approaches $r^2$, which allows us to simplify the equation in the far field.

$E=\frac{1}{2\pi {ϵ}_0}\frac{p}{r^3}$

Note that one can use the binomial theorem just as in the section above to find out where this far field approximation (x>>a) is valid.

Finding the electric field associated with a dipole anywhere on a plane

Now that you've solved for two special cases and determined that the dipole field falls off as $\frac{1}{r^3}$ at great distances (referred to as the far field), it is instructive to find the field's behavior off the axis.

Consider the case of an electric dipole's field at a point $P$ with the coordinates $(x,y)$ as represented in the figure. Note that we can represent the coordinates either as Cartesian, or as cylindrical.

dipole field in a plane.

$r_1=\sqrt{{(y+a)}^2+x^2}\cos \alpha =\frac{y+a}{\sqrt{{(y+a)}^2+x^2}}\sin \alpha =\frac{x}{\sqrt{{(y+a)}^2+x^2}}$

$r_2=\sqrt{{(y-a)}^2+x^2}\cos \beta =\frac{y-a}{\sqrt{{(y-a)}^2+x^2}}\sin \beta =\frac{x}{\sqrt{{(y-a)}^2+x^2}}$

In Cartesian coordinates the electric field at any point in the plane from each charge can be found as follows:

${E_r}_1=\frac{1}{4\pi {ϵ}_0}\frac{+q}{{(y+a)}^2+x^2}{E_r}_2=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y-a)}^2+x^2}$

We can apply the principle of superposition and add the fields from each of the charges, remembering that they are vectors so that the vertical components add to vertical and horizontal add to horizontal.

First finding the horizontal coordinates labeled as $E_x$:

${{E_r}_1}_x=\frac{1}{4\pi {ϵ}_0}\frac{+q}{{(y+a)}^2+x^2}\sin \alpha =\frac{1}{4\pi {ϵ}_0}\frac{+q}{{(y+a)}^2+x^2}\frac{x}{\sqrt{{(y+a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{+qx}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}$

${{E_r}_2}_x=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y-a)}^2+x^2}\sin \beta =\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y-a)}^2+x^2}\frac{x}{\sqrt{{y-a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{-qx}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}$

Next finding the vertical components for each of the two charges labeled as $E_y$ we obtain:

${{E_r}_1}_y=\frac{1}{4\pi {ϵ}_0}\frac{+q}{{(y+a)}^2+x^2}\cos \alpha =\frac{1}{4\pi {ϵ}_0}\frac{+q}{{(y+a)}^2+x^2}\frac{y+a}{\sqrt{{(y+a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{+q(y+a)}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}$

${{E_r}_2}_y=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y-a)}^2+x^2}\cos \beta =\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y-a)}^2+x^2}\frac{y-a}{\sqrt{{y-a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{-q(y-a)}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}$

Summing the horizontal components yields:

$E_x=\frac{1}{4\pi {ϵ}_0}q[\frac{x}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}-\frac{x}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}]$

And for large r (either large x, large y, or their combination) this becomes:

$E_x=\frac{qa}{2\pi {ϵ}_0}\frac{1}{r^3}$

Summing the vertical components yields:

$E_y=\frac{1}{4\pi {ϵ}_0}q[\frac{y+a}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}-\frac{y-a}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}]$

Finding the electric field associated with an electric quadrupole

Figure 3 - one form of electric quadrupole

The electric field measured at point along the vertical axis due to any single charge along the horizontal axis (shown in Figure 3) is:

$E_q=\frac{q}{4\pi {ϵ}_o{r}^2}$

So the center charges contribute:

$E_{2q}=\frac{2q}{4\pi {ϵ}_o{r}^2}$

While the left and right charges contribute a total field of magnitude:

$E_{-q}=\frac{-q}{4\pi {ϵ}_o(r^2+d^2)}$

By inspection we can see that the horizontal components of the electric field cancel out. Only the vertical components are left. So we multiply by

$sin\theta =\frac{r}{\sqrt{r^2+d^2}}$

To get the vertical component of the electric field for a single negative charge:

$E_{-q}=\frac{-q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

And for the two negative charges together we get:

$E_{-2q}=\frac{-2q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

Now we can add to obtain the total vertical component of the electric field.

$E=E_{2q}+E_{-2q}=\frac{2q}{4\pi {ϵ}_o{r}^2}+\frac{-2q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

Which simplifies to:

$E=\frac{q}{2\pi {ϵ}_o}[\frac{1}{r^2}-\frac{r}{{(r^2+d^2)}^{\frac{3}{2}}}]$

Factoring out r³ from the denominator's final term yields:

$E=\frac{q}{2\pi {ϵ}_o}[\frac{1}{r^2}-\frac{r}{{r^3(1+(\frac{d}{r}{)}^2)}^{\frac{3}{2}}}]$

Which reduces to:

$E=\frac{q}{2\pi {ϵ}_o{r}^2}[1-\frac{1}{{(1+(\frac{d}{r}{)}^2)}^{\frac{3}{2}}}]$

So now we have a perfectly good equation for calculating the field. An engineer might think that sufficient since they can calculate the value when they need it, but a physicist would like to know how this behaves in the "far field" where r >> d. Fortunately we have a tool - our friend the binomial expansion - which allows us to answer the far field question, as follows:

$[1-\frac{1}{{(1+(\frac{d}{r}{)}^2)}^{\frac{3}{2}}}]=[1-{(1+{\left(\frac{d}{r}\right)}^2)}^{-\frac{3}{2}}]=[1-(1-\frac{3}{2}{\left(\frac{d}{r}\right)}^2)+...]=\frac{3}{2}{\left(\frac{d}{r}\right)}^2$

Substituting back into the original equation:

$E=\frac{q}{2\pi {ϵ}_o{r}^2}\frac{3}{2}{\left(\frac{d}{r}\right)}^2$

Simplifying, we find that in the far field when r >> d the electric field from a quadrupole falls off as $\frac{1}{r^4}$

$E=\frac{3q{d}^2}{4\pi {ϵ}_o{r}^4}$

Electric field associated with a line charge

1. A very long solid nonconducting cylinder of radius R₀ and length L (R₀ << L) possesses a uniform volume charge density ρ_E (C/m³). For points far from the ends and for which r << L,
   1. Find electric fields for all r, distance from axis of cylinder. You may need separate expressions for r < R₀ and r > R₀. Show that electric field is continuous at r = R₀, i.e. two expressions for electric fields agree at r = R₀.
   2. Describe the motion of a small free charge Q of opposite sign (i.e. Q ρ_E < 0) placed inside the cylinder. Find the frequency of oscillation $\nu$ if the charge oscillates about the axis of cylinder. (Note: $\nu$, frequency, has units of cycles / second, while $\omega$, angular frequency, has units of radians / second.)
   3. Let's change the problem and say we have a cylindrical shell of charge (of radius R₀, and σ_E so that the total charge remains the same). How do the expressions for electric fields change for either regions r < R₀ or r > R₀? Is the electric field still continuous? Give a plausible argument why we might not expect electric field to be continuous.

Find the electric field for a finite line with uniform unit charge of λ coulombs per unit length

an infinite line with uniform unit charge.

The figure shows an finitely long line chage with linear charge density of $\lambda =\frac{dq}{dx}$. The charge extends from x = -a to x = +b which are arbitrary (although not infinite) and are not shown on the figure.

Just as it the derivation for the infinite lint, the magnitude of the electric field which results from a short section dx of this line charge as measured at point P is a result of the charge $dq=\lambda dx$:

And with that charge we can calculate the field contribution (dE) from dq as:

$dE=\frac{1}{4\pi {ϵ}_0}\frac{dq}{r^2}=\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}$           (1)

We can no longer argue by symmetry that the electric field will be the same at any point of equal separation from the infinite line charge, so we can solve this in detail, which we will do using 2 dimensions. Once we have a solution for 2 dimensions, simple rotation around the line charge will allow us to determine the field in the 3rd dimension.

The electric field is a vector which we'll represent as $d\overrightarrow{E}$. This we'll separate into 2-dimensional Cartesian components:

$d{E}_x=-dE\sin \theta$      and      $d{E}_y=dE\cos \theta$

The sign of the electric field at $d{E}_x$ indicates the $d{\overrightarrow{E}}_x$ location of the point with respect to x.

We find the total electric field for the horizontal $E_x$ and vertical $E_y$ components to determine $\overrightarrow{E}$ at the point P by integrating. Note that $\sin \theta$ is used to find the components of the field horizontally, while $\cos \theta$ is used to find them vertically.

$E_x=\int d{E}_x=-\underset{x=-a}{\overset{x=+b}{\int }}\sin \theta dE$

and

$E_y=\int d{E}_y=\underset{x=-a}{\overset{x=+b}{\int }}\cos \theta dE$

Or in full vectorial form:

$\overrightarrow{E}=\underset{L}{\int }d\overrightarrow{E}=\underset{L}{\int }\frac{1}{4\pi {ϵ}_0}\frac{dq}{r^2}\overrightarrow{u_r}=\underset{L}{\int }\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{r^2}\overrightarrow{u_r}$

In this example the distance, r, from the charge to point P can be expressed in terms of Cartesian coordinates x and y.

$r=\sqrt{x^2+y^2}$.

which allows us to calculation the magnitude of the electric field at point P from the charge dx at r using the equation. $dE=\frac{1}{4\pi {ϵ}_0}=\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}$

$\sin \theta =\frac{opposite}{hypotenuse}=\frac{x}{\sqrt{x^2+y^2}}$          and         $\cos \theta =\frac{adjacent}{hypotenuse}=\frac{y}{\sqrt{x^2+y^2}}$

However we must recall that that magnitude corresponds to the vector $d\overrightarrow{E}$, which changes as one moves along the line. So we must find the component of $d\overrightarrow{E}$ which points in the x or in the y directions.

To find the component in the x direction $d{E}_x=-dE\sin \theta$ and to find it in the y direction apply $d{E}_y=dE\cos \theta$.

The x component of the field $d{\overrightarrow{E}}_x$ can be found by integrating from one end of the line source at -a to the other at a. If the line source is equally long to left and right, the net field in the x direction will cancel as below.

$E_x=\int d{E}_x=-\underset{x=-a}{\overset{x=+b}{\int }}\sin \theta dE=-\underset{x=-a}{\overset{x=+b}{\int }}\frac{x}{\sqrt{x^2+y^2}}dE$

$E_x=\underset{x=-a}{\overset{x=+b}{\int }}\frac{x}{\sqrt{x^2+y^2}},\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}$        (2)

$E=\frac{\lambda }{4\pi {ϵ}_0}\underset{x=-a}{\overset{x=+b}{\int }}\frac{xdx}{{\left[x^2+y^2\right]}^{\frac{3}{2}}}$           (3)

$E_x=\frac{\lambda }{4\pi {ϵ}_0}[-\frac{1}{{[a^2+y^2]}^{\frac{1}{2}}}+\frac{1}{{[b^2+y^2]}^{\frac{1}{2}}}]$        (4)

hold 1

Similarly the y component of the field $d{\overrightarrow{E}}_y$ can be found by integrating from one end of the line source at -a to the other at a.

$E_y=\int d{E}_y=\underset{x=-a}{\overset{x=+b}{\int }}\cos \theta dE=\underset{x=-a}{\overset{x=+b}{\int }}\frac{y}{\sqrt{x^2+y^2}}dE$

And substituting in the equation above we get:

$E_y=\underset{x=-a}{\overset{x=+b}{\int }}\frac{y}{\sqrt{x^2+y^2}}\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}=\frac{\lambda y}{4\pi {ϵ}_0}\underset{x=-a}{\overset{x=+b}{\int }}\frac{dx}{{[x^2+y^2]}^{\frac{3}{2}}}$        (5)

$E_y=\frac{\lambda y}{4\pi {ϵ}_0}\underset{x=-a}{\overset{x=+b}{\int }}\frac{dx}{{[x^2+y^2]}^{\frac{3}{2}}}$        (6)

$E_y=\frac{\lambda }{4\pi {ϵ}_{0}y}{\left[\frac{x}{{[x^2+y^2]}^{\frac{1}{2}}}\right]}_{x=-a}^{x=+b}$        (7)

Find the electric field for an infinite line with uniform unit charge of λ coulombs per unit length

an infinite line with uniform unit charge.

The figure shows an infinitely long line chage with linear charge density of $\lambda =\frac{dq}{dx}$.

The magnitude of the electric field which results from a short section dx of this line charge as measured at point P is a result of the charge $dq=\lambda dx$:

And with that charge we can calculate the field contribution (dE) from dq as:

$dE=\frac{1}{4\pi {ϵ}_0}\frac{dq}{r^2}=\frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}$           (1)

Since we can argue by symmetry that the electric field will be the same at any point of equal separation from the infinite line charge, we can solve this in using 2 dimensions. Once we have a solution for 2 dimensions, simple rotation around the line charge will provide the field in the 3rd dimension.

The electric field is a vector which we'll represent as $d\overrightarrow{E}$. This we'll separate into 2-dimensional Cartesian components:

$d{E}_x=-dE\sin \theta$      and      $d{E}_y=dE\cos \theta$

The sign of the electric field at $d{E}_x$ indicates the $d{\overrightarrow{E}}_x$ location of the point with respect to x.

We find the total electric field for the horizontal $E_x$ and vertical $E_y$ components to determine $\overrightarrow{E}$ at the point P by integrating. Note that $\sin \theta$ is used to find the components of the field horizontally, while $\cos \theta$ is used to find them vertically.

$E_x=\int d{E}_x=-\underset{x=-\mathrm{\infty }}{\overset{x=+\mathrm{\infty }}{\int }}\sin \theta dE$

and

$E_y=\int d{E}_y=\underset{x=-\mathrm{\infty }}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta dE$

In these expressions $E_x$> must integrate to zero because every element of charge to the left of the perpendicular point P has a corresponding element on the right so that their contributions to the field in the horizontal direction cancel each other. So $\overrightarrow{E}$ points in the vertical direction only. As for the electric field contributions to $E_y$, the right half and left half of the charged lines will make an equal contribution, so we can write:

$E=E_y=2\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta dE$

Substituting the expression (1) above into this equation we get:

$E=2\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta \frac{1}{4\pi {ϵ}_0}\frac{\lambda dx}{x^2+y^2}=\frac{\lambda }{2\pi {ϵ}_0}\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta \frac{dx}{x^2+y^2}$          (2)

By definition $\tan \theta =\frac{x}{y}$, which we can write as $x=y\tan \theta$. Differentiating this expression yields: $dx=y{\sec }^2\theta d\theta$. Substitute this into (2) and you will get:

$E=\frac{\lambda }{2\pi {ϵ}_0}\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta \frac{y{\sec }^2\theta d\theta }{x^2+y^2}=\frac{\lambda }{2\pi {ϵ}_0}\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\frac{y}{x^2+y^2}\cos \theta {\sec }^2\theta d\theta$      (3)

Applying further trigonometric relationships: $\cos \theta =\frac{y}{r}$,    $\sec \theta =\frac{r}{y}$    and    $x^2+y^2=r^2$,     we can establish equivalencies:

$\frac{y}{x^2+y^2}\cos \theta {\sec }^2\theta d\theta =\frac{y}{r^2}\frac{y}{r}\frac{r^2}{y^2}=\frac{y}{ry}=\frac{\cos \theta }{y}$

Which can the be substituted into equation (3) to yield a significantly simplified integral:

$E=\frac{\lambda }{2\pi {ϵ}_{0}y}\underset{x=0}{\overset{x=+\mathrm{\infty }}{\int }}\cos \theta d\theta$

To evaluate this we need only observe that $x\to 0$, $\theta \to 0$ and similarly $x\to +\mathrm{\infty }$, $\theta \to \frac{\pi }{2}$, to simplify our range of integration to:

$E=\frac{\lambda }{2\pi {ϵ}_{0}y}\underset{\theta =0}{\overset{\theta =\frac{\pi }{2}}{\int }}\cos \theta d\theta =\frac{\lambda }{2\pi {ϵ}_{0}y}[\sin \frac{\pi }{2}-\sin 0]=\frac{\lambda }{2\pi {ϵ}_{0}y}$

Which yields a final solution:

$E=\frac{\lambda }{2\pi {ϵ}_{0}y}$

And this can be generalized for any point at distance r from the line charge to:

$E=\frac{\lambda }{2\pi {ϵ}_{0}r}$