This Quantum World/Appendix/Calculus

Differential calculus: a very brief introduction

Another method by which we can obtain a well-defined, finite number from infinitesimal quantities is to divide one such quantity by another.

We shall assume throughout that we are dealing with well-behaved functions, which means that you can plot the graph of such a function without lifting up your pencil, and you can do the same with each of the function's derivatives. So what is a function, and what is the derivative of a function?

A function $f(x)$ is a machine with an input and an output. Insert a number $x$ and out pops the number $f(x).$ Rather confusingly, we sometimes think of $f(x)$ not as a machine that churns out numbers but as the number churned out when $x$ is inserted.

The (first) derivative $f^{\prime }(x)$ of $f(x)$ is a function that tells us how much $f(x)$ increases as $x$ increases (starting from a given value of $x,$ say $x_0$) in the limit in which both the increase $\mathrm{\Delta }x$ in $x$ and the corresponding increase $\mathrm{\Delta }f=f(x+\mathrm{\Delta }x)-f(x)$ in $f(x)$ (which of course may be negative) tend toward 0:

$f^{\prime }(x_0)=\underset{\mathrm{\Delta }x\to 0}{\lim }\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}=\frac{df}{dx}(x_0).$

The above diagrams illustrate this limit. The ratio $\mathrm{\Delta }f/\mathrm{\Delta }x$ is the slope of the straight line through the black circles (that is, the $\tan$ of the angle between the positive $x$ axis and the straight line, measured counterclockwise from the positive $x$ axis). As $\mathrm{\Delta }x$ decreases, the black circle at $x+\mathrm{\Delta }x$ slides along the graph of $f(x)$ towards the black circle at $x,$ and the slope of the straight line through the circles increases. In the limit $\mathrm{\Delta }x\to 0,$ the straight line becomes a tangent on the graph of $f(x),$ touching it at $x.$ The slope of the tangent on $f(x)$ at $x_0$ is what we mean by the slope of $f(x)$ at $x_0.$

So the first derivative $f^{\prime }(x)$ of $f(x)$ is the function that equals the slope of $f(x)$ for every $x.$ To differentiate a function $f$ is to obtain its first derivative $f^{\prime }.$ By differentiating $f^{\prime },$ we obtain the second derivative $f^{″}=\frac{d^{2}f}{d{x}^2}$ of $f,$ by differentiating $f^{″}$ we obtain the third derivative $f^{‴}=\frac{d^{3}f}{d{x}^3},$ and so on.

It is readily shown that if $a$ is a number and $f$ and $g$ are functions of $x,$ then

$\frac{d(af)}{dx}=a\frac{df}{dx}$  and  $\frac{d(f+g)}{dx}=\frac{df}{dx}+\frac{dg}{dx}.$

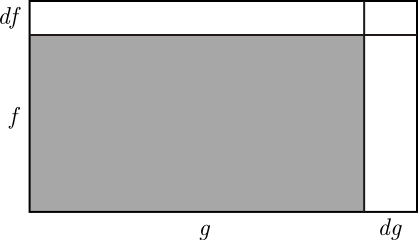
A slightly more difficult problem is to differentiate the product $e=fg$ of two functions of $x.$ Think of $f$ and $g$ as the vertical and horizontal sides of a rectangle of area $e.$ As $x$ increases by $\mathrm{\Delta }x,$ the product $fg$ increases by the sum of the areas of the three white rectangles in this diagram:

In other "words",

$\mathrm{\Delta }e=f(\mathrm{\Delta }g)+(\mathrm{\Delta }f)g+(\mathrm{\Delta }f)(\mathrm{\Delta }g)$

and thus

$\frac{\mathrm{\Delta }e}{\mathrm{\Delta }x}=f\frac{\mathrm{\Delta }g}{\mathrm{\Delta }x}+\frac{\mathrm{\Delta }f}{\mathrm{\Delta }x}g+\frac{\mathrm{\Delta }f\mathrm{\Delta }g}{\mathrm{\Delta }x}.$

If we now take the limit in which $\mathrm{\Delta }x$ and, hence, $\mathrm{\Delta }f$ and $\mathrm{\Delta }g$ tend toward 0, the first two terms on the right-hand side tend toward $f{g}^{\prime }+f^{\prime }g.$ What about the third term? Because it is the product of an expression (either $\mathrm{\Delta }f$ or $\mathrm{\Delta }g$) that tends toward 0 and an expression (either $\mathrm{\Delta }g/\mathrm{\Delta }x$ or $\mathrm{\Delta }f/\mathrm{\Delta }x$) that tends toward a finite number, it tends toward 0. The bottom line:

$e^{\prime }=(fg{)}^{\prime }=f{g}^{\prime }+f^{\prime }g.$

This is readily generalized to products of $n$ functions. Here is a special case:

$(f^n{)}^{\prime }=f^{n-1}{f}^{\prime }+f^{n-2}{f}^{\prime }f+f^{n-3}{f}^{\prime }{f}^2+\cdots +f^{\prime }{f}^{n-1}=n{f}^{n-1}{f}^{\prime }.$

Observe that there are $n$ equal terms between the two equal signs. If the function $f$ returns whatever you insert, this boils down to

$(x^n{)}^{\prime }=n{x}^{n-1}.$

Now suppose that $g$ is a function of $f$ and $f$ is a function of $x.$ An increase in $x$ by $\mathrm{\Delta }x$ causes an increase in $f$ by $\mathrm{\Delta }f\approx \frac{df}{dx}\mathrm{\Delta }x,$ and this in turn causes an increase in $g$ by $\mathrm{\Delta }g\approx \frac{dg}{df}\mathrm{\Delta }f.$ Thus $\frac{\mathrm{\Delta }g}{\mathrm{\Delta }x}\approx \frac{dg}{df}\frac{df}{dx}.$ In the limit $\mathrm{\Delta }x\to 0$ the $\approx$ becomes a $=$ :

$\frac{dg}{dx}=\frac{dg}{df}\frac{df}{dx}.$

---

We obtained $(x^n{)}^{\prime }=n{x}^{n-1}$ for integers $n\ge 2.$ Obviously it also holds for $n=0$ and $n=1.$

1. Show that it also holds for negative integers $n.$ Hint: Use the product rule to calculate $(x^n{x}^{-n}{)}^{\prime }.$
2. Show that $(\sqrt{x}{)}^{\prime }=1/(2\sqrt{x}).$ Hint: Use the product rule to calculate $(\sqrt{x}\sqrt{x}{)}^{\prime }.$
3. Show that $(x^n{)}^{\prime }=n{x}^{n-1}$ also holds for $n=1/m$ where $m$ is a natural number.
4. Show that this equation also holds if $n$ is a rational number. Use $\frac{dg}{dx}=\frac{dg}{df}\frac{df}{dx}.$

Since every real number is the limit of a sequence of rational numbers, we may now confidently proceed on the assumption that $(x^n{)}^{\prime }=n{x}^{n-1}$ holds for all real numbers $n.$