Timeless Theorems of Mathematics/Pythagorean Theorem

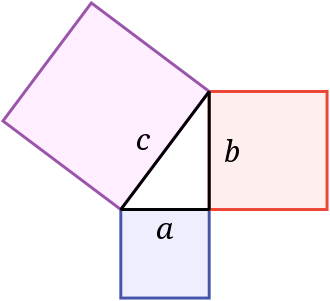
The Pythagorean Theorem is a fundamental relation between the three sides of a right triangle in Euclidean Geometry. It states that the square of the hypotenuse side is equal to the sum of squares of the other two sides in a right-angled triangle.

In this right triangle, $a^2+b^2=c^2$ according to the Pythagorean Theorem

The theorem is named after the Greek philosopher Pythagoras (570 – 495 BC). But, both the Egyptians and the Babylonians were aware of versions of the Pythagorean theorem about 1500 years before Pythagoras.

Proof

Statement

In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the two other sides.

Proof with the help of two right angled triangles

Proposition : Let in the triangle $ABC,\mathrm{\angle }B=90$°, the hypotenuse $AC=b,$ $AB=c$ and $BC=a$. It is required to prove that $A{C}^2=A{B}^2+B{C}^2,$ i.e. $b^2=c^2+a^2$.

Construction : Produce $BC$ up to $D$ in such a way that $CD=AB=c$. Also, draw perpendicular $DE$ at $D$ on $BC$ produced, so that $DE=BC=a$. Join $C,E$ and $A,E$.

James A. Garfield's Proof of the Pythagorean Theorem using a Trapezoid

Proof : In $\mathrm{\Delta }ABC$ and $\mathrm{\Delta }CDE$, $AB=CD=c,BC=DE=a$ and included $\mathrm{\angle }ABC$ = included $\mathrm{\angle }CDE$ [As $\mathrm{\angle }ABC=\mathrm{\angle }CDE=90$°]

Therefore, $\mathrm{\Delta }ABC\cong \mathrm{\Delta }CDR$. [Side-Angle-Side theorem]

∴$AC=CE=b$ and $\mathrm{\angle }BAC=\mathrm{\angle }ECD$.

Again, since $AB\perp BD$ and $ED\perp BD,AB\parallel ED$. Therefore, $ABDE$ is a trapezoid.

$\mathrm{\angle }ABC+\mathrm{\angle }BAC+\mathrm{\angle }ACB=180$°

or, $90$°$+\mathrm{\angle }BAC+\mathrm{\angle }ACB=180$°

or, $\mathrm{\angle }BAC+\mathrm{\angle }ACB=90$°

or, $\mathrm{\angle }RCD+\mathrm{\angle }ACB=90$° [As $\mathrm{\angle }BAC=\mathrm{\angle }ECD$]

Again, $\mathrm{\angle }BCD=180$°

or, $\mathrm{\angle }BCA+\mathrm{\angle }ACE+\mathrm{\angle }ECD=180$°

or $\mathrm{\angle }ACE=90$°

∴$\mathrm{\Delta }ACE$ is a right triangle.

Now, Trapezoid $ABDE=\mathrm{\Delta }ABC+\mathrm{\Delta }CDE+\mathrm{\Delta }ACE$

or, $\frac{1}{2}BD(AB+DE)=\frac{1}{2}(AB)(BC)+\frac{1}{2}(CD)(DE)+\frac{1}{2}(AC)(CE)$

or, $\frac{1}{2}(a+c)(c+a)=\frac{1}{2}ac+\frac{1}{2}ac+\frac{1}{2}{b}^2$

or, $\frac{1}{2}(a+c{)}^2=\frac{1}{2}(2ac+b^2)$

or, $(a+c{)}^2=(2ac+b^2)$

or, $a^2+2ac+c^2=2ac+b^2$

or, $b^2=a^2+c^2$ [Proved]

[Note : The 12th President of the United States of America, James A. Garfield proved the Pythagorean Theorem with the help of two right angled triangles. His proof of the Pythagorean Theorem was published on page 161 of the New-England Journal of Education, April 1, 1876]

Proof with the help of Algebra

Proposition : Let, in the triangle $c$ is the hypotenuse and $a,b$ be the two other sides. It is required to prove that, $c^2=a^2+b^2$.

Pythagorean Theorem's Proof with Algebra

Construction : Draw four triangles congruent to $\mathrm{\Delta }ABC$ as shown in the figure.

Proof : The large shape in the figure is a square with an area of $(a+b{)}^2$ [As teh length of every side is same, $(a+b)$ and the angles are right angles]

The area of the small quadrilateral is $c^2$, as the shape is a square. [As, every side is $c$ and every angle of the quadrilateral is right angle (proved while proving with the help of two right angled triangles)]

According to the figure, $(a+b{)}^2=4(\frac{1}{2}ab)+c^2$

Or, $a^2+2ab+b^2=2ab+c^2$

Or, $a^2+b^2=c^2$ [Proved]